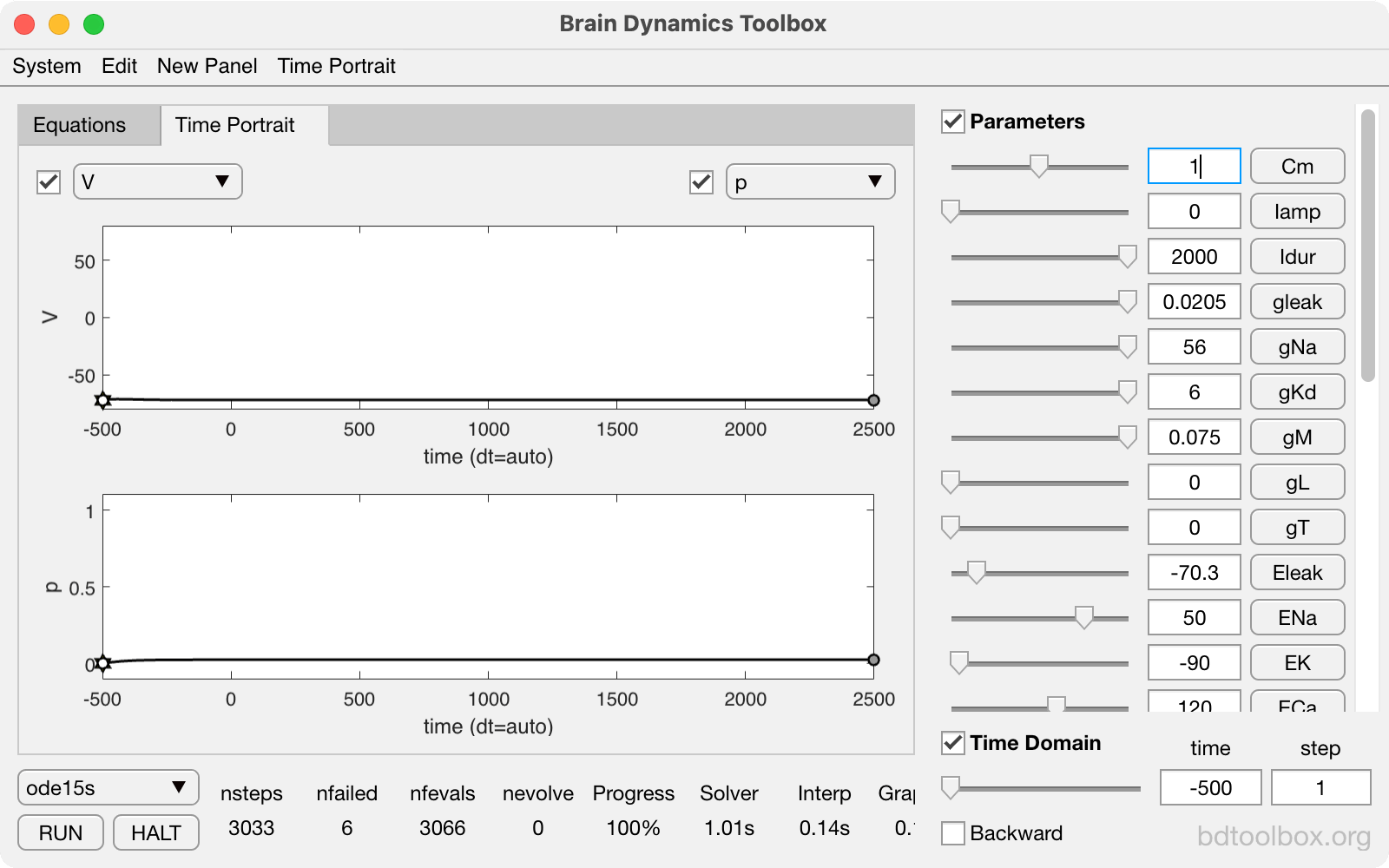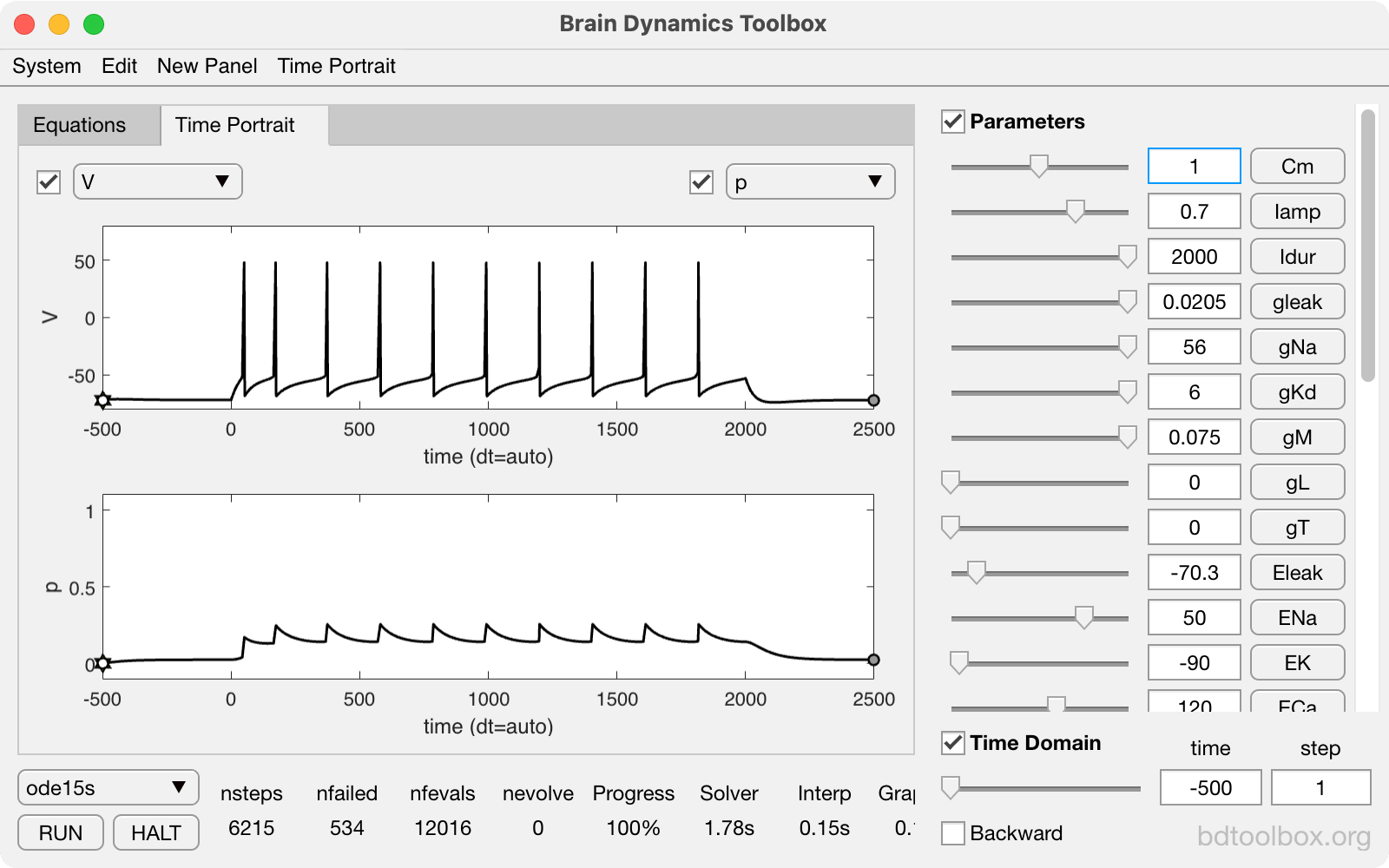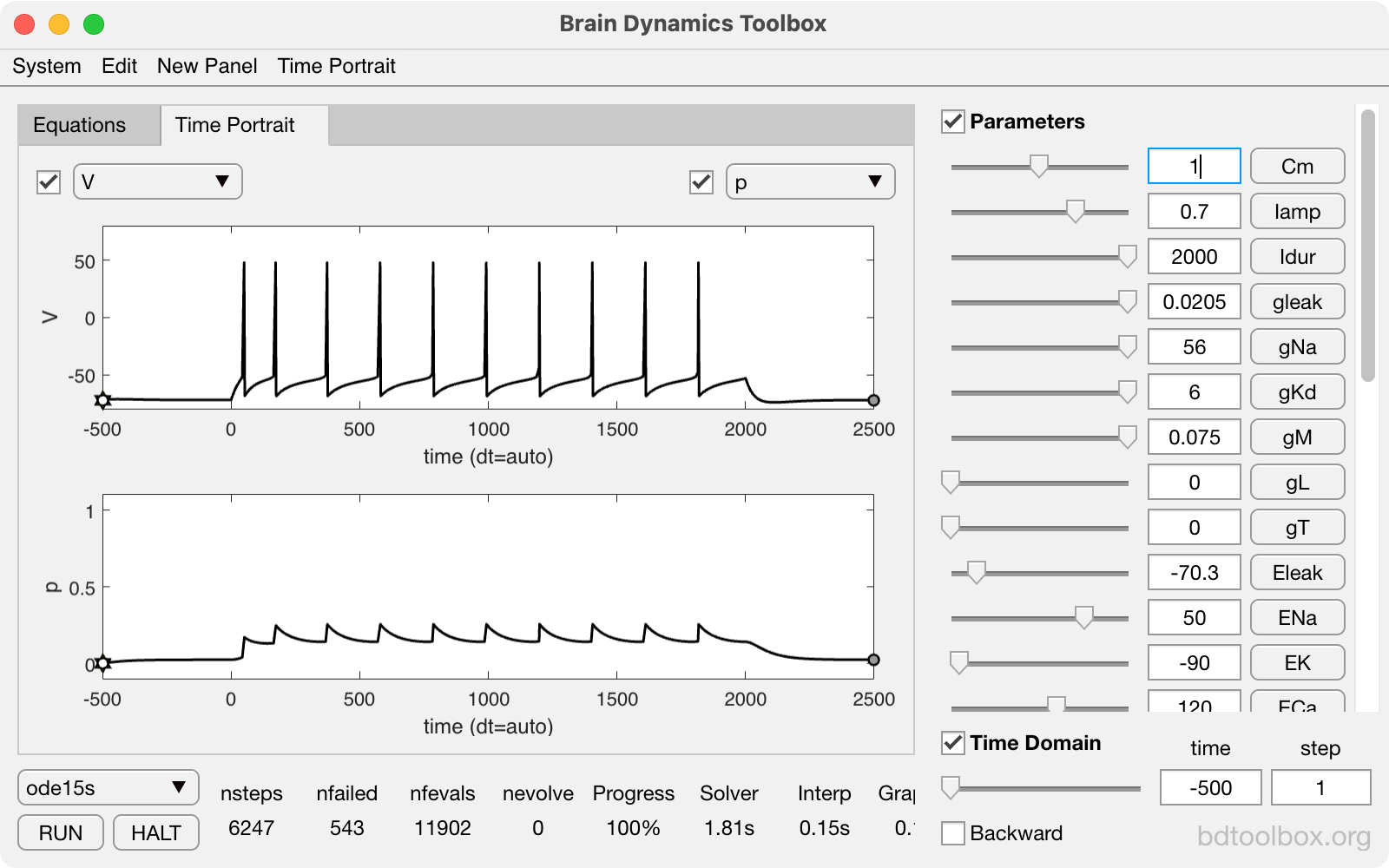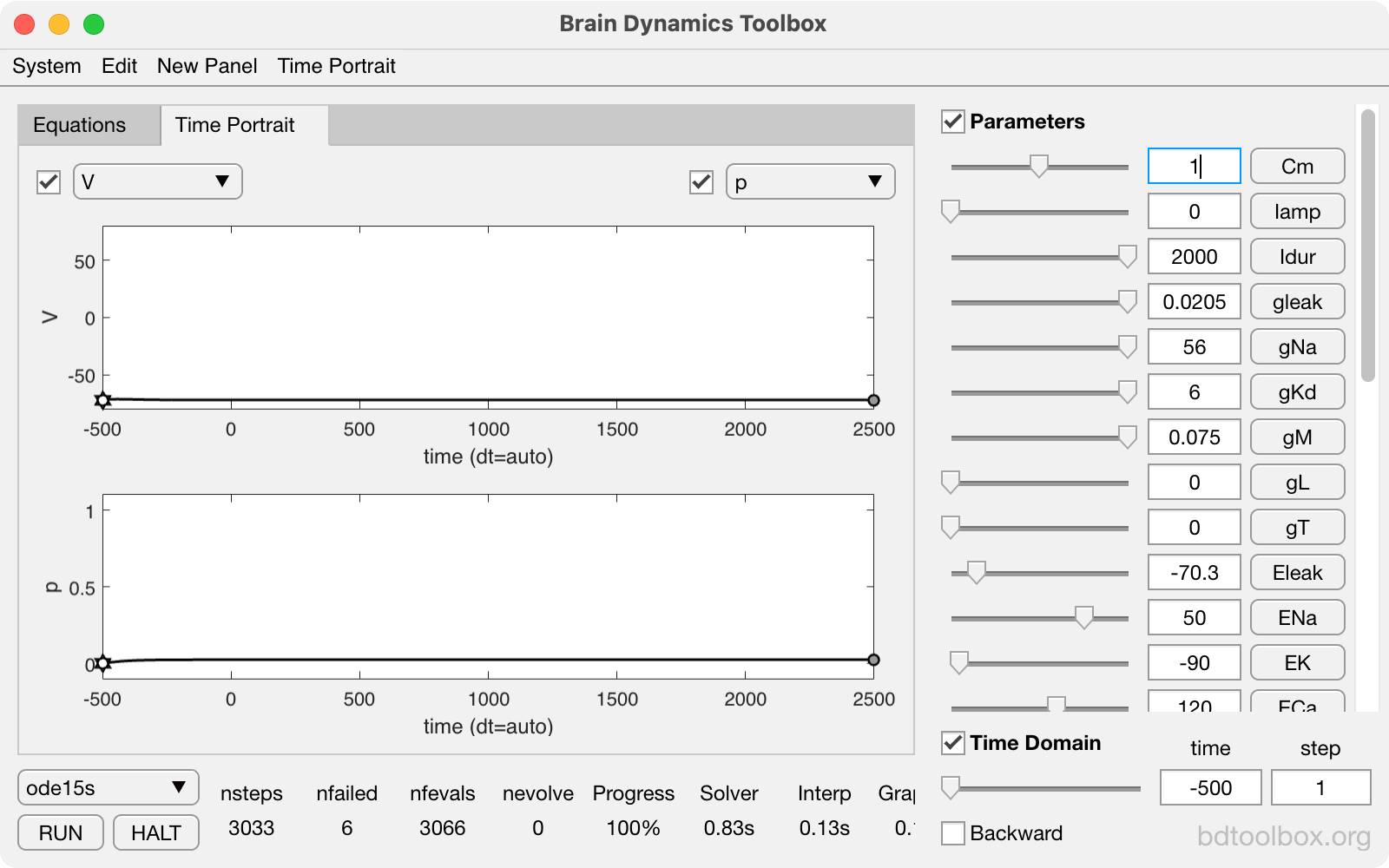
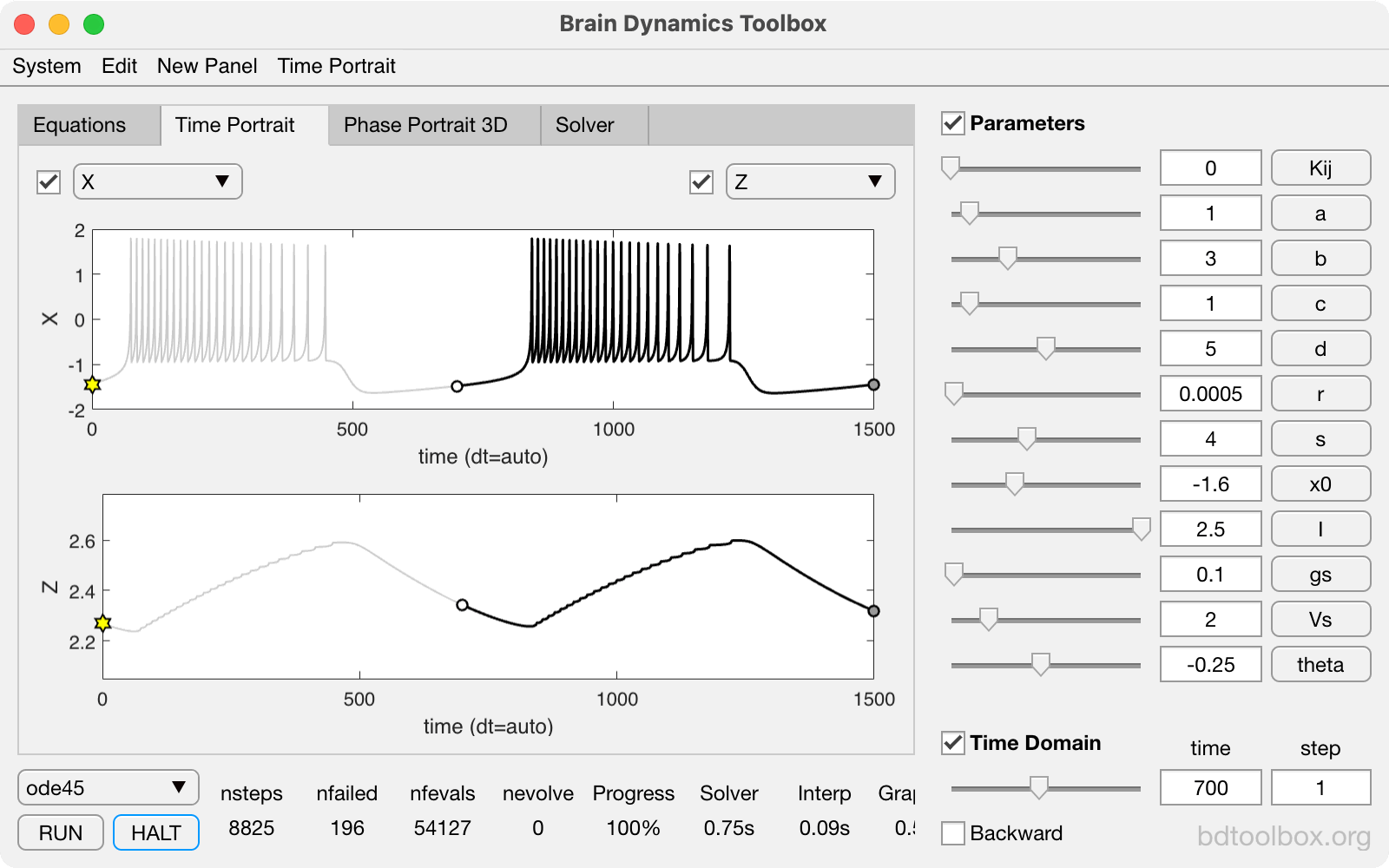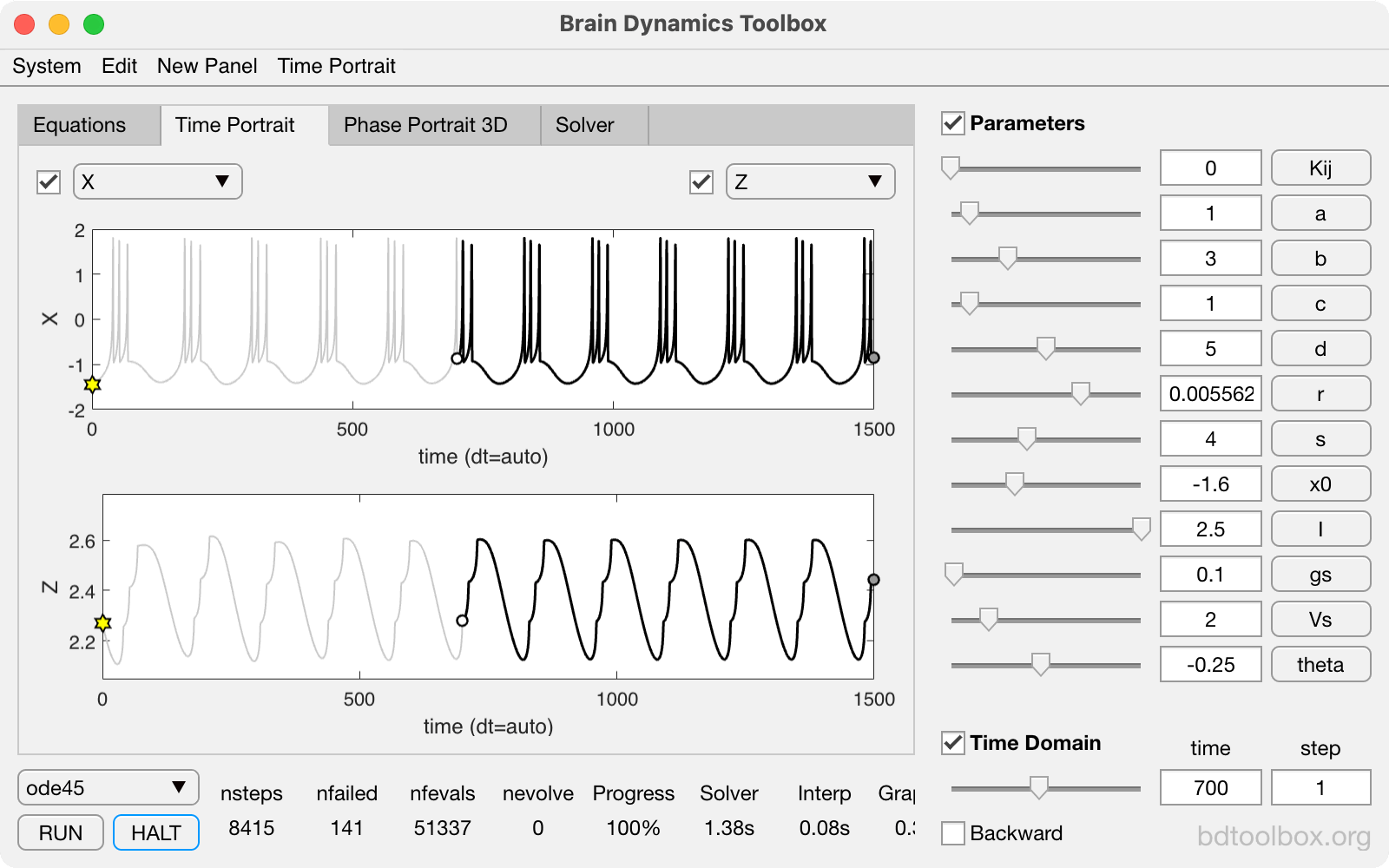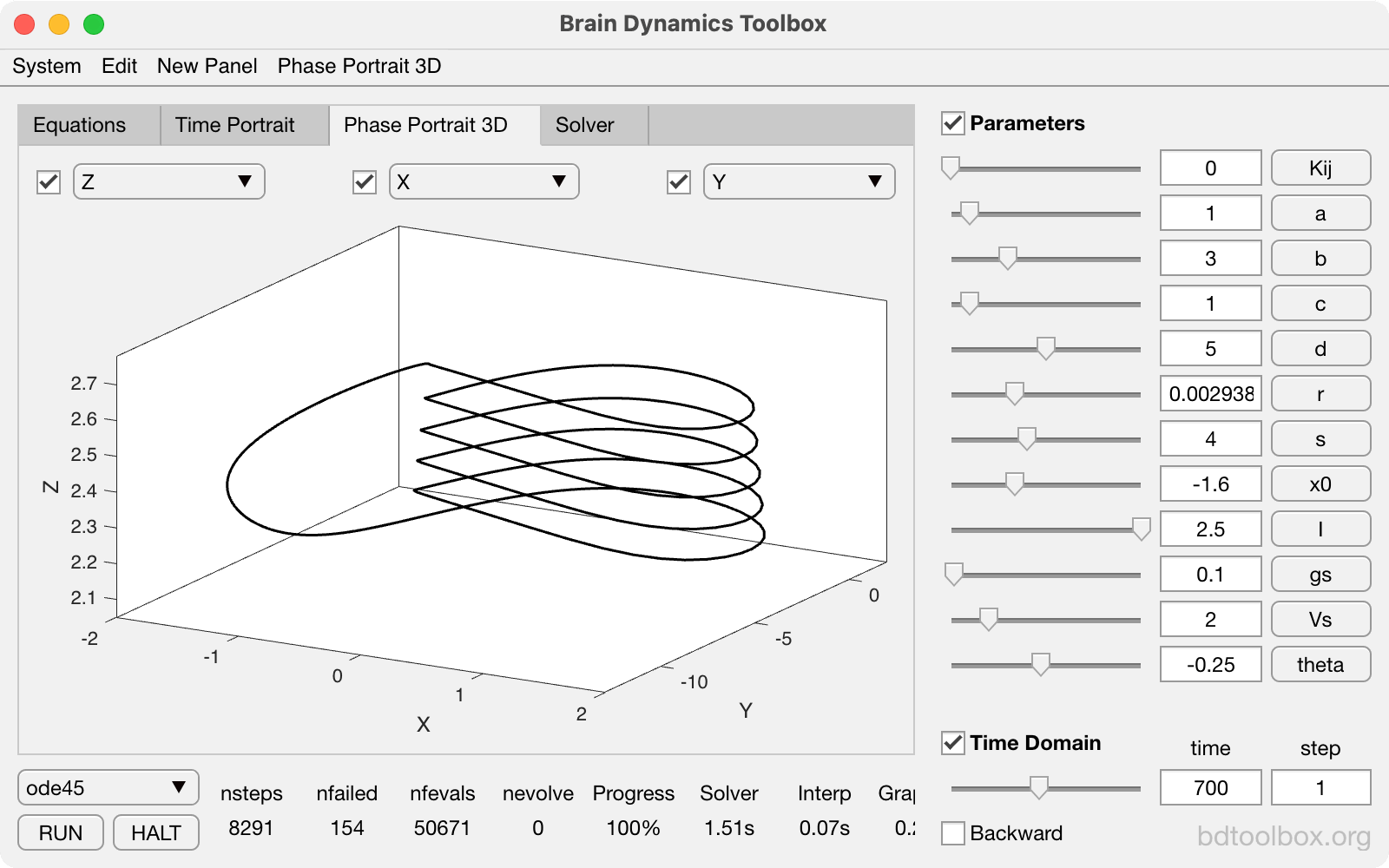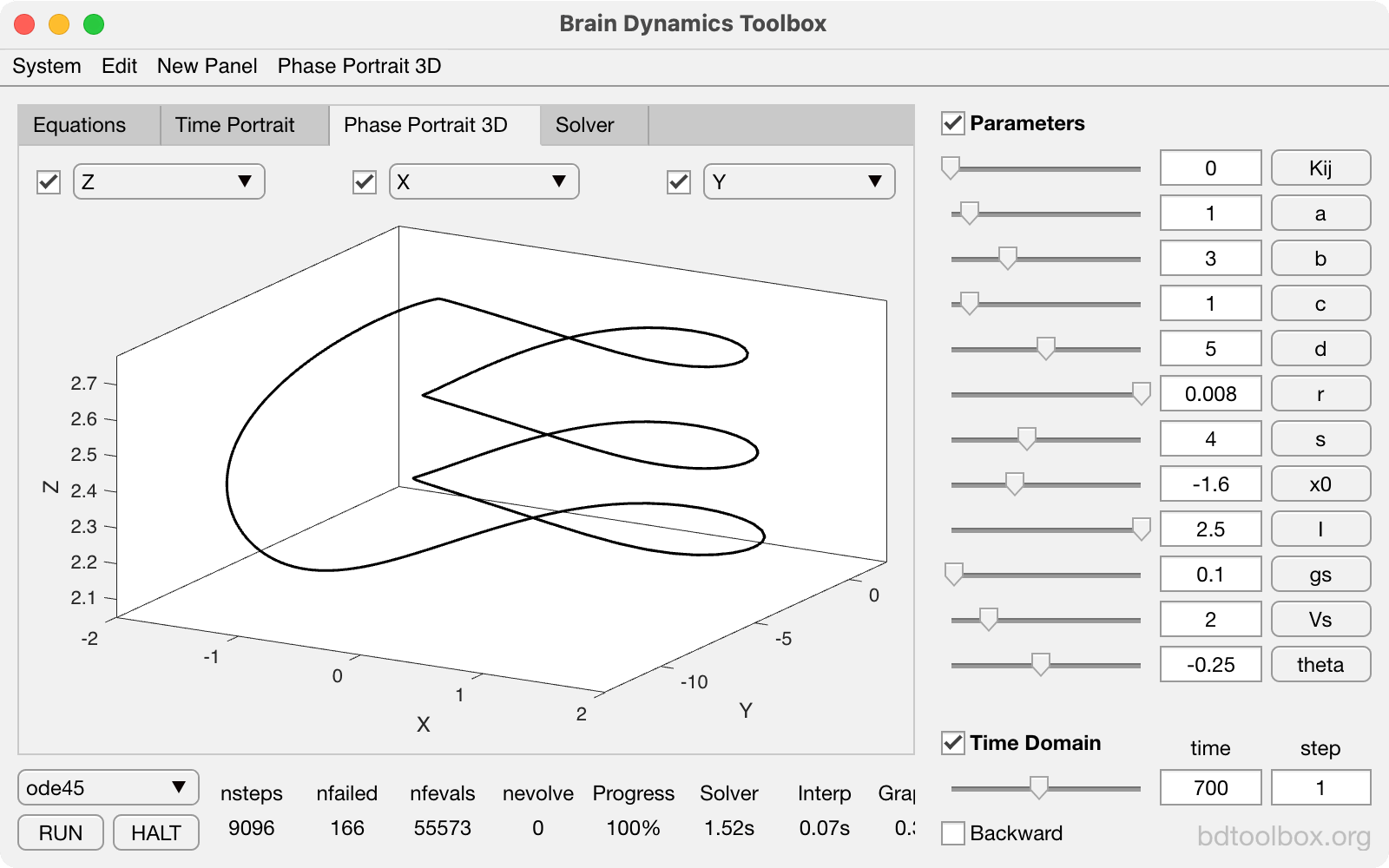
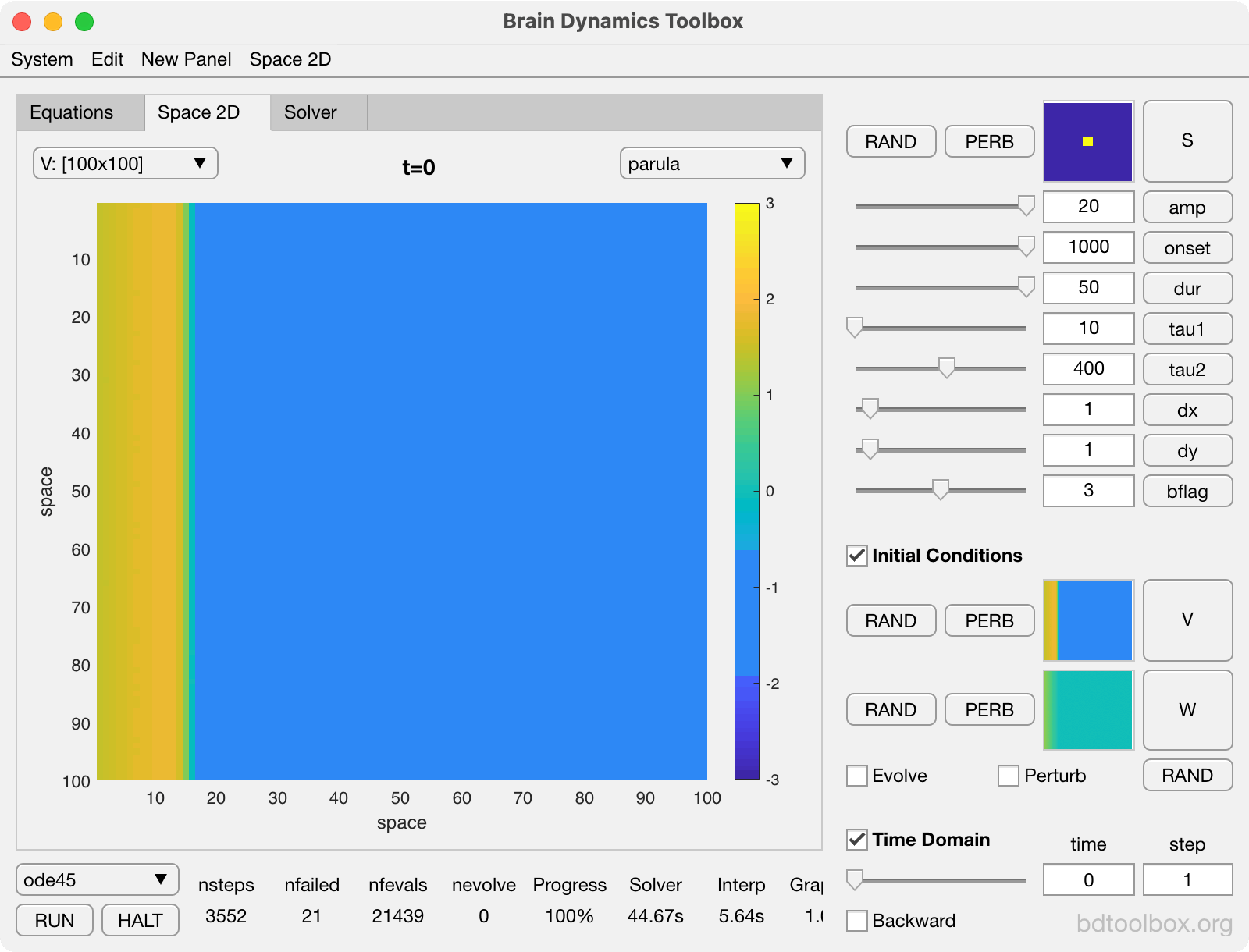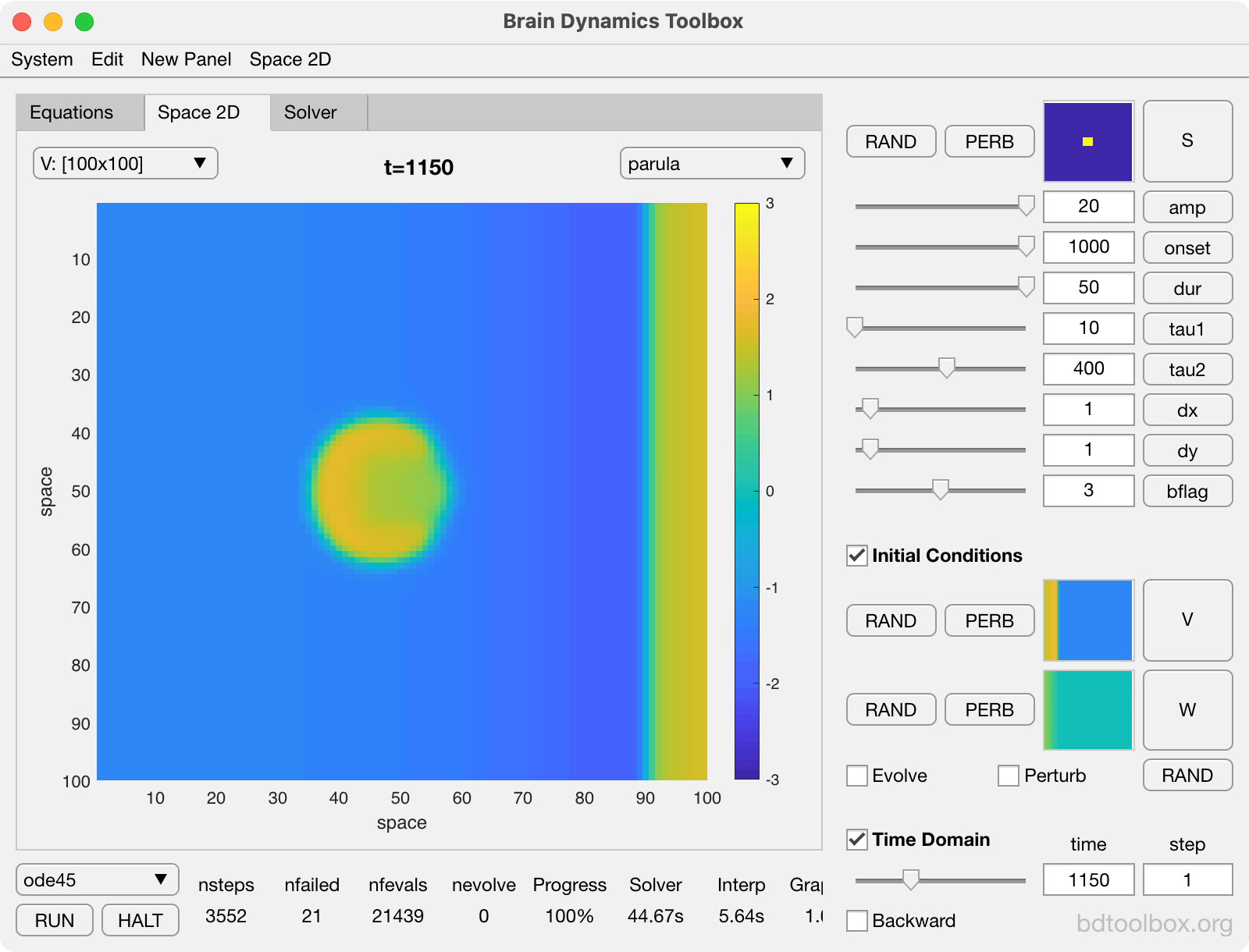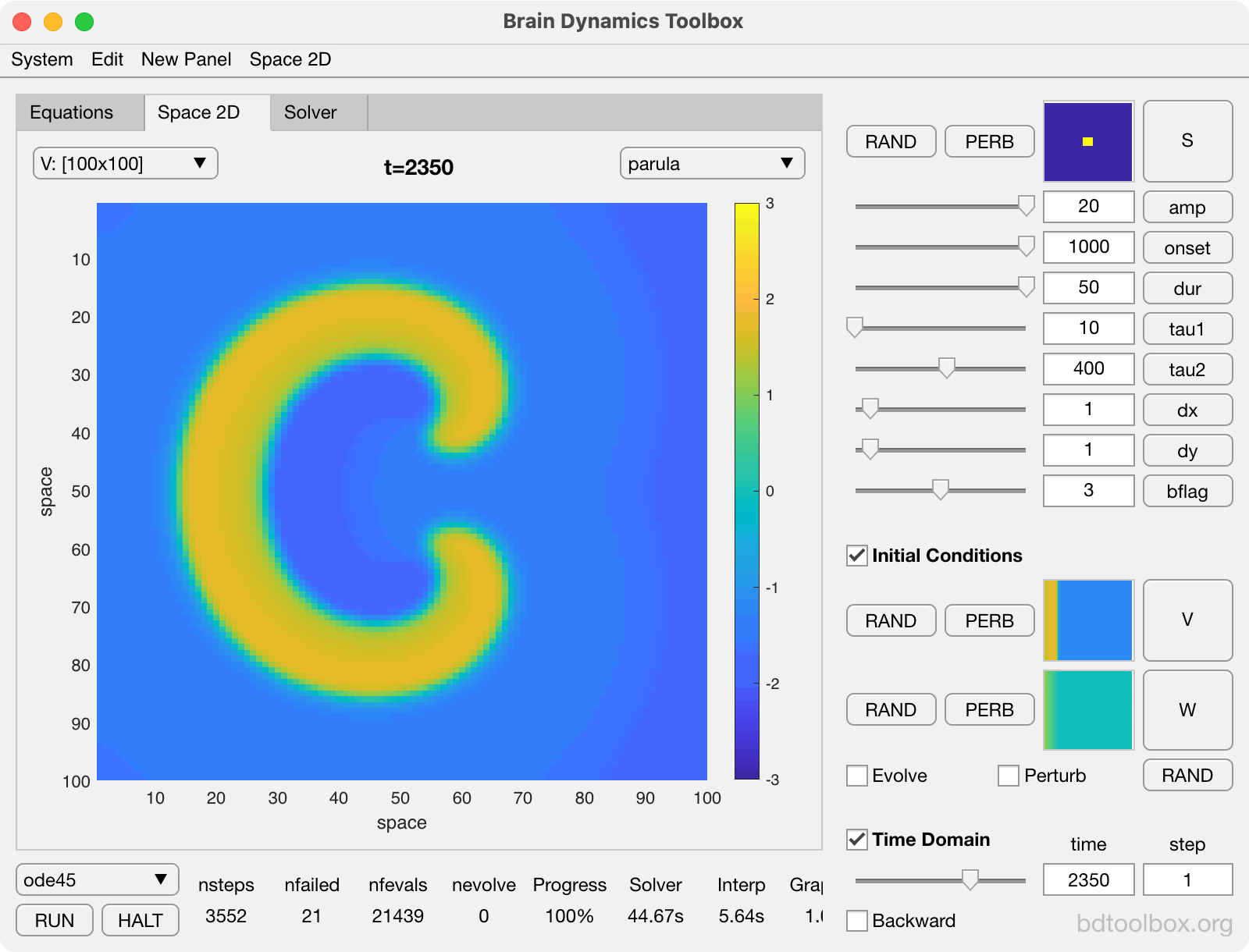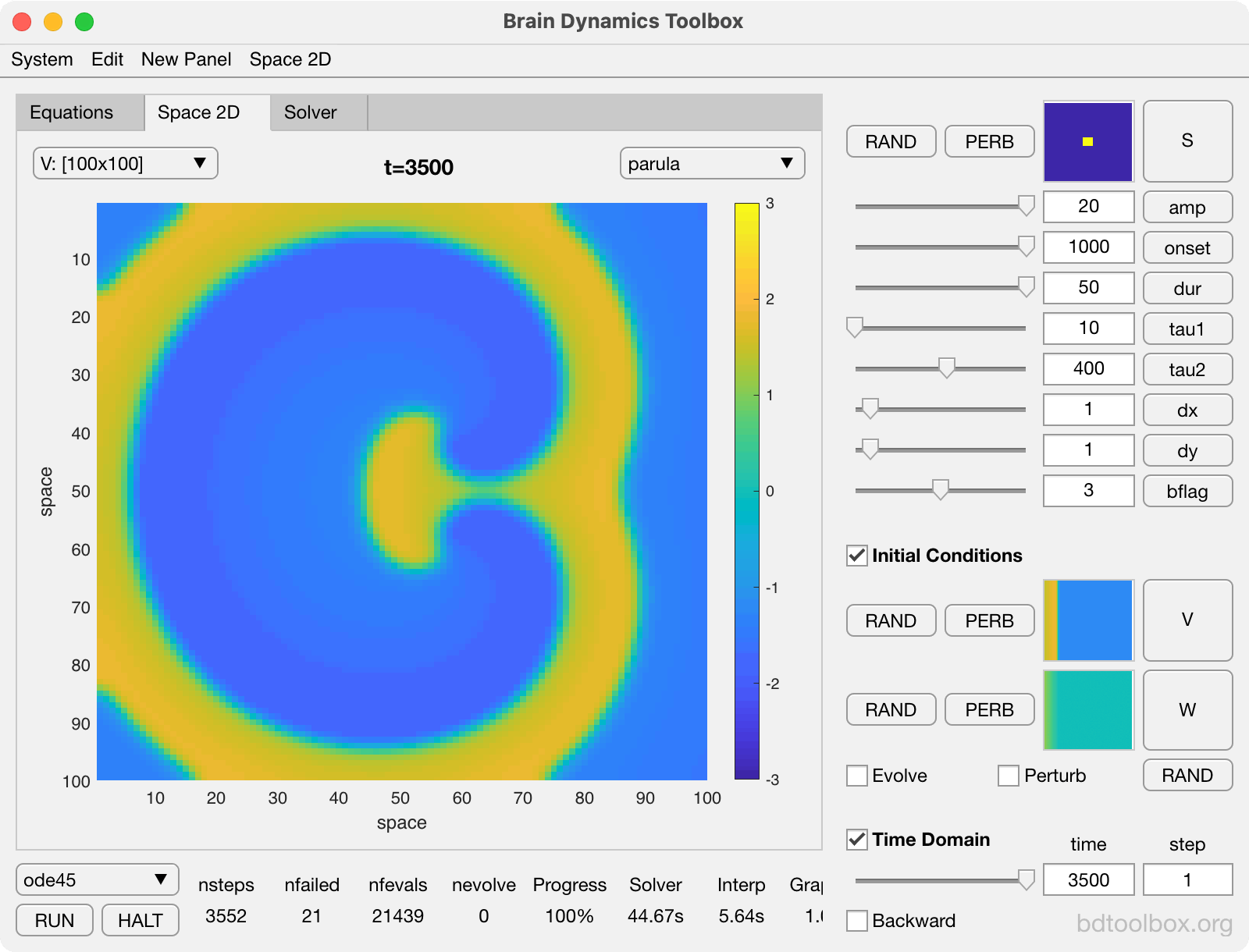
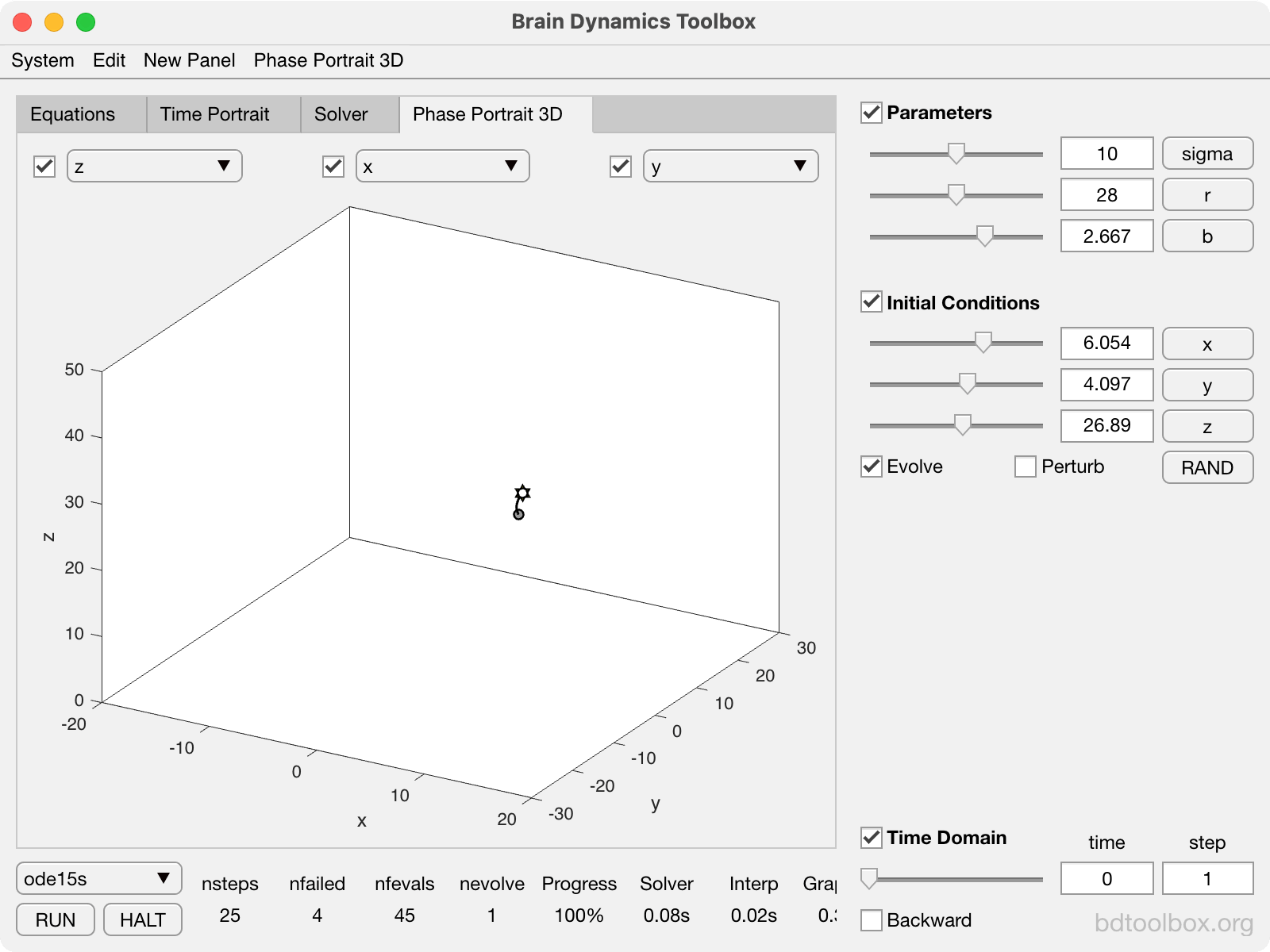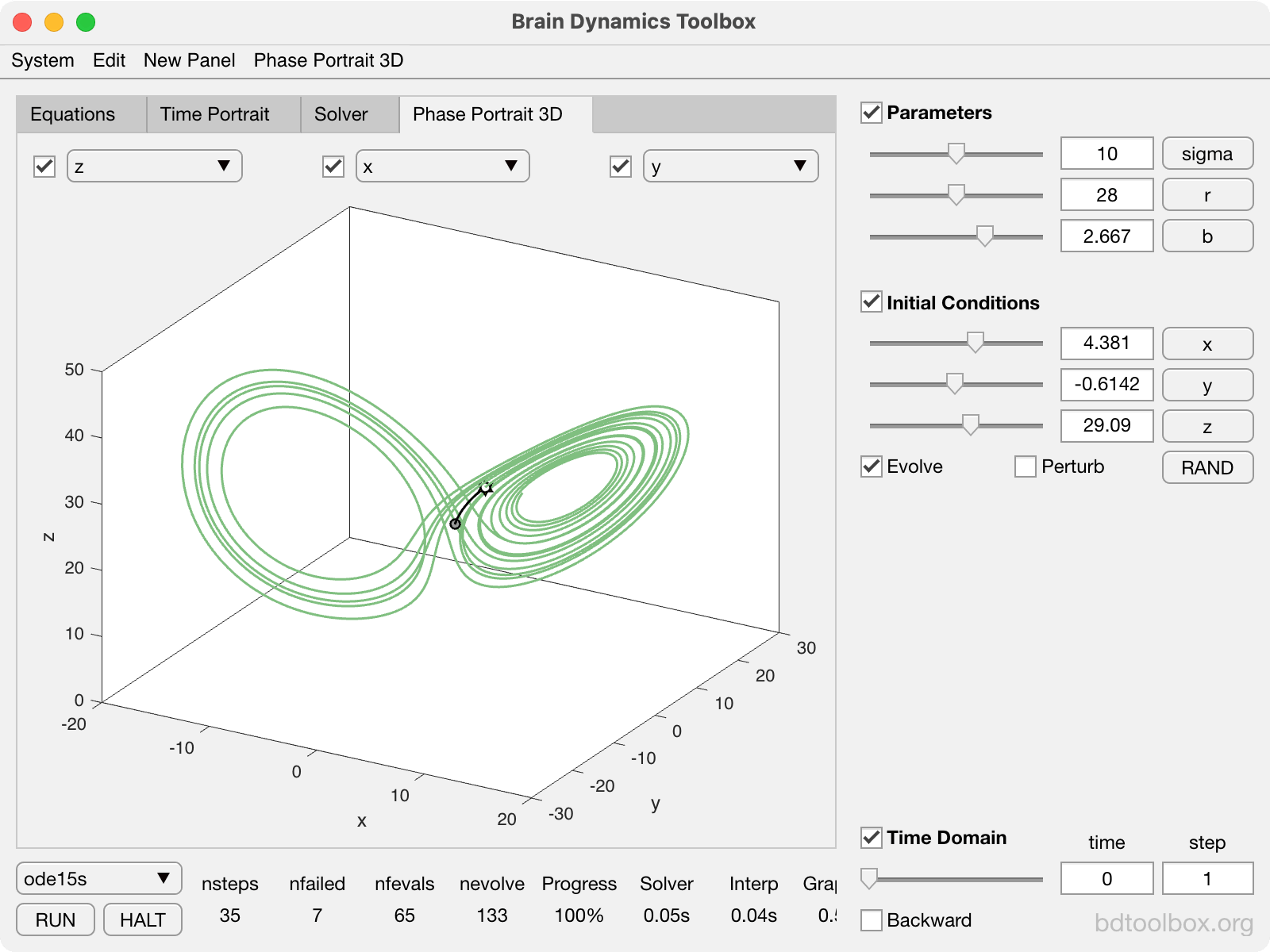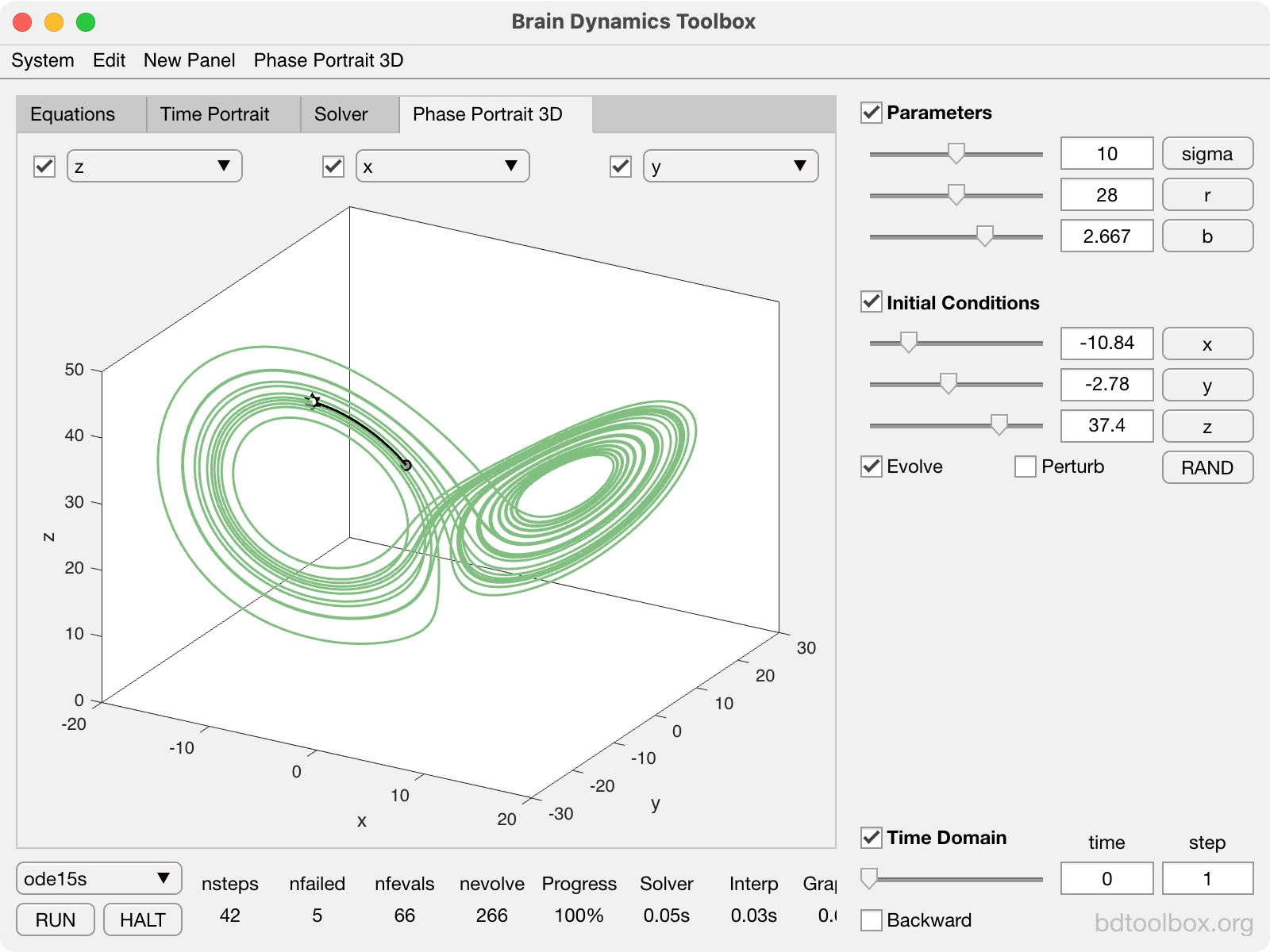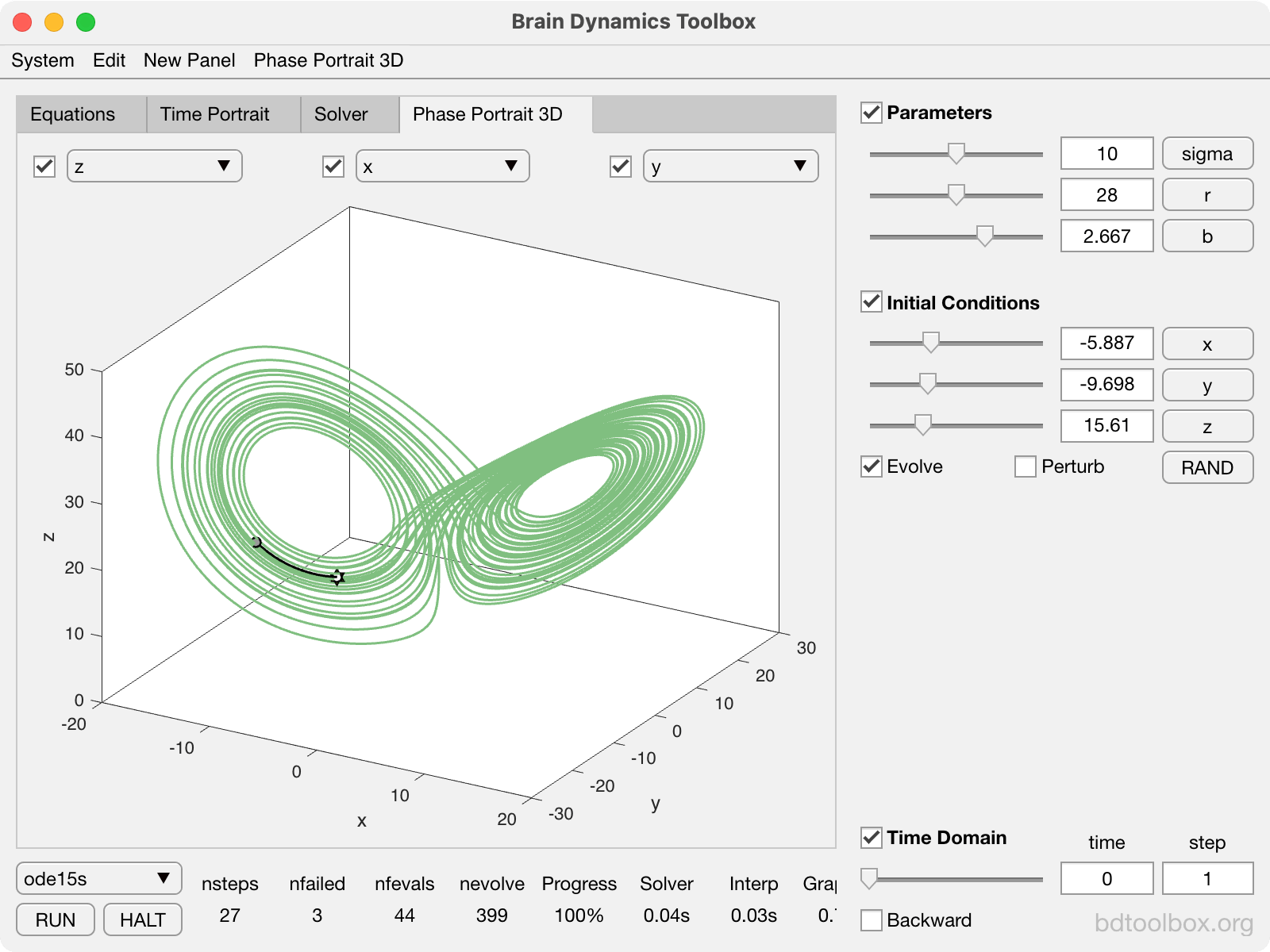
Point Neurons

	Bistability in the Hodgkin-Huxley model of the action potential in squid axon.
	Supercritical Hopf bifurction in the Morris-Lecar model of barnacle muscle.
	Saddle-Node bifurcation on a Limit Cycle in the Morris-Lecar model.
	Regular spiking in a minimal neural model by Pospischil, et al.
	Intrinsic Bursting in the Hindmarsh-Rose neuron.

---

Neural Masses

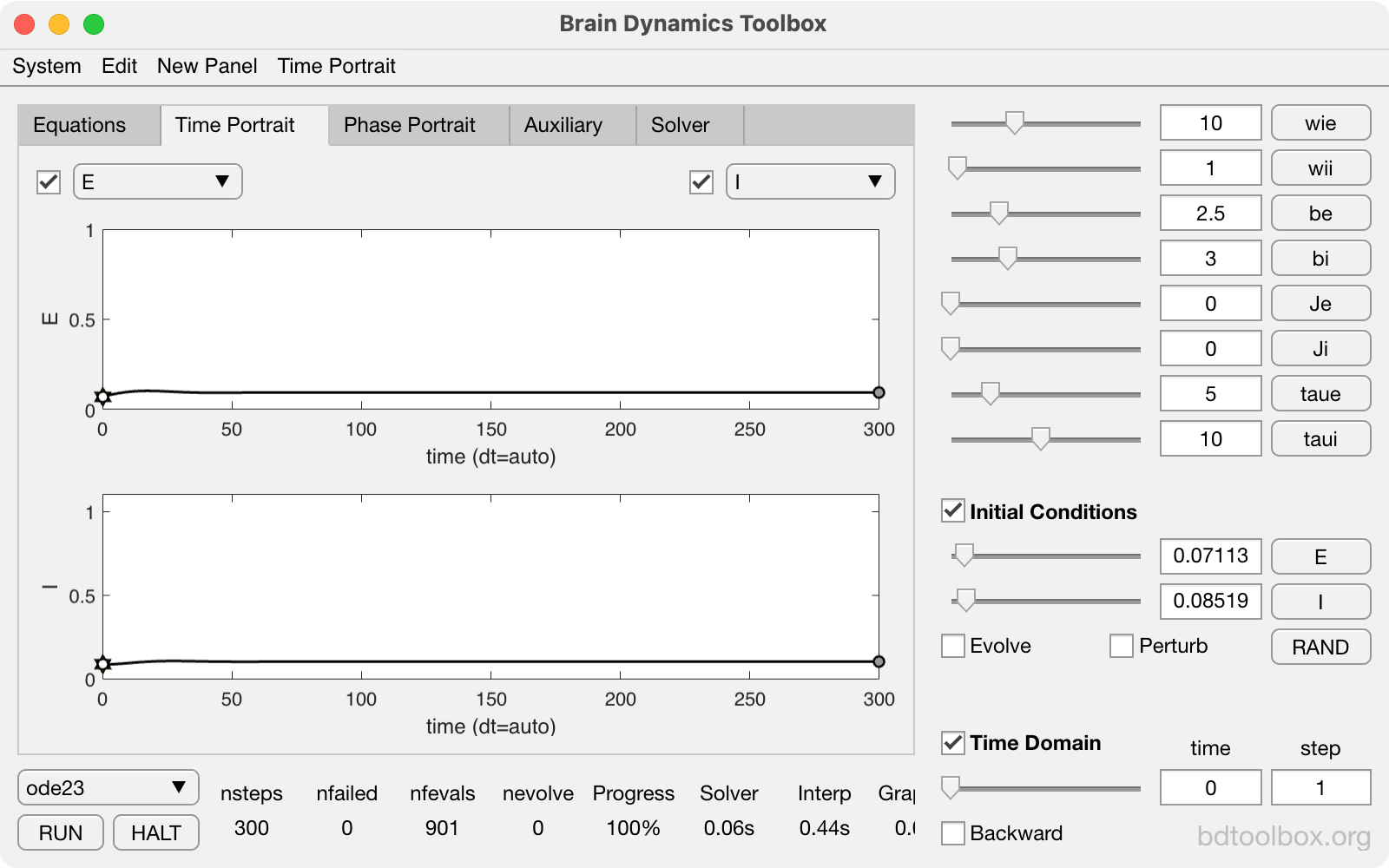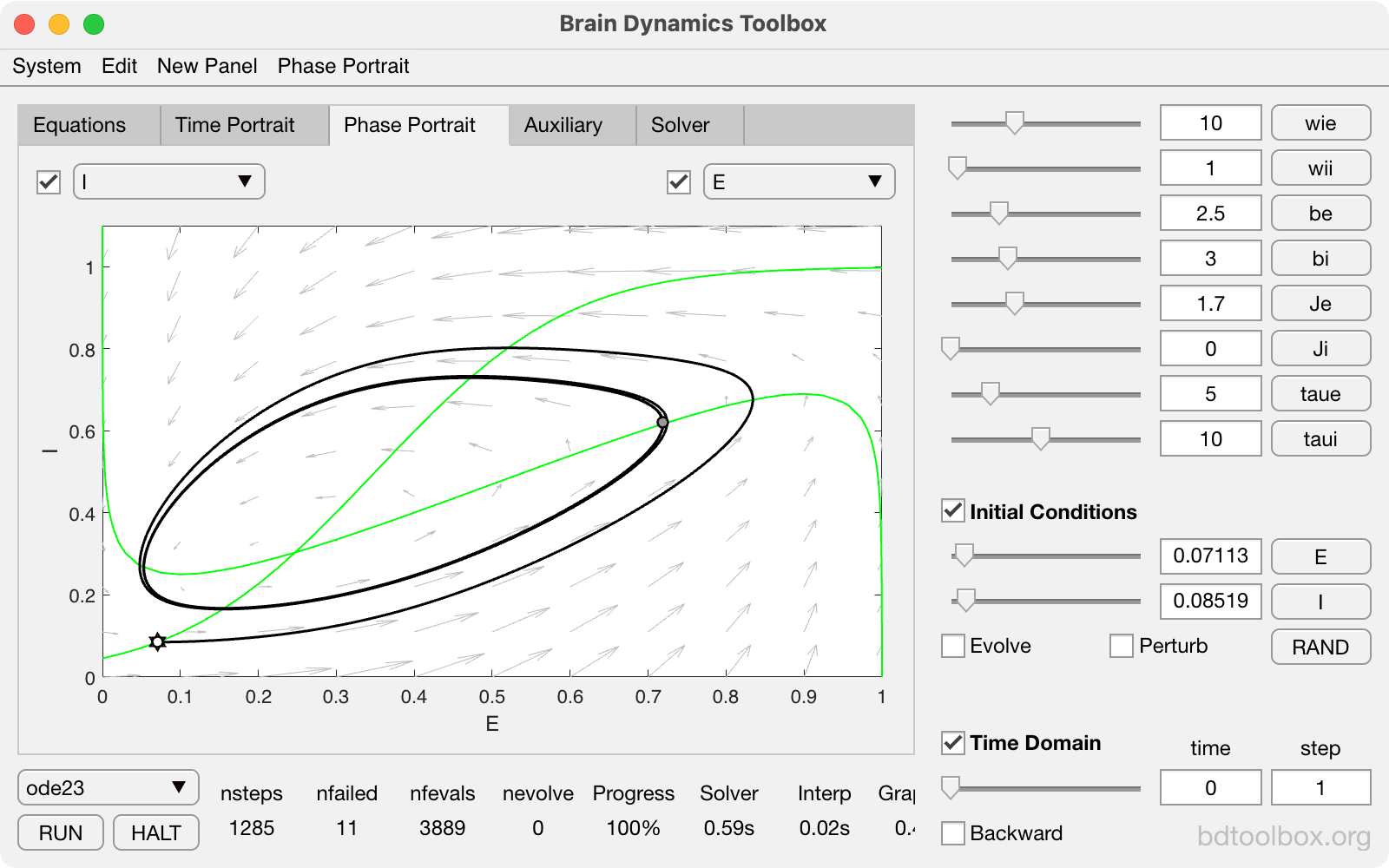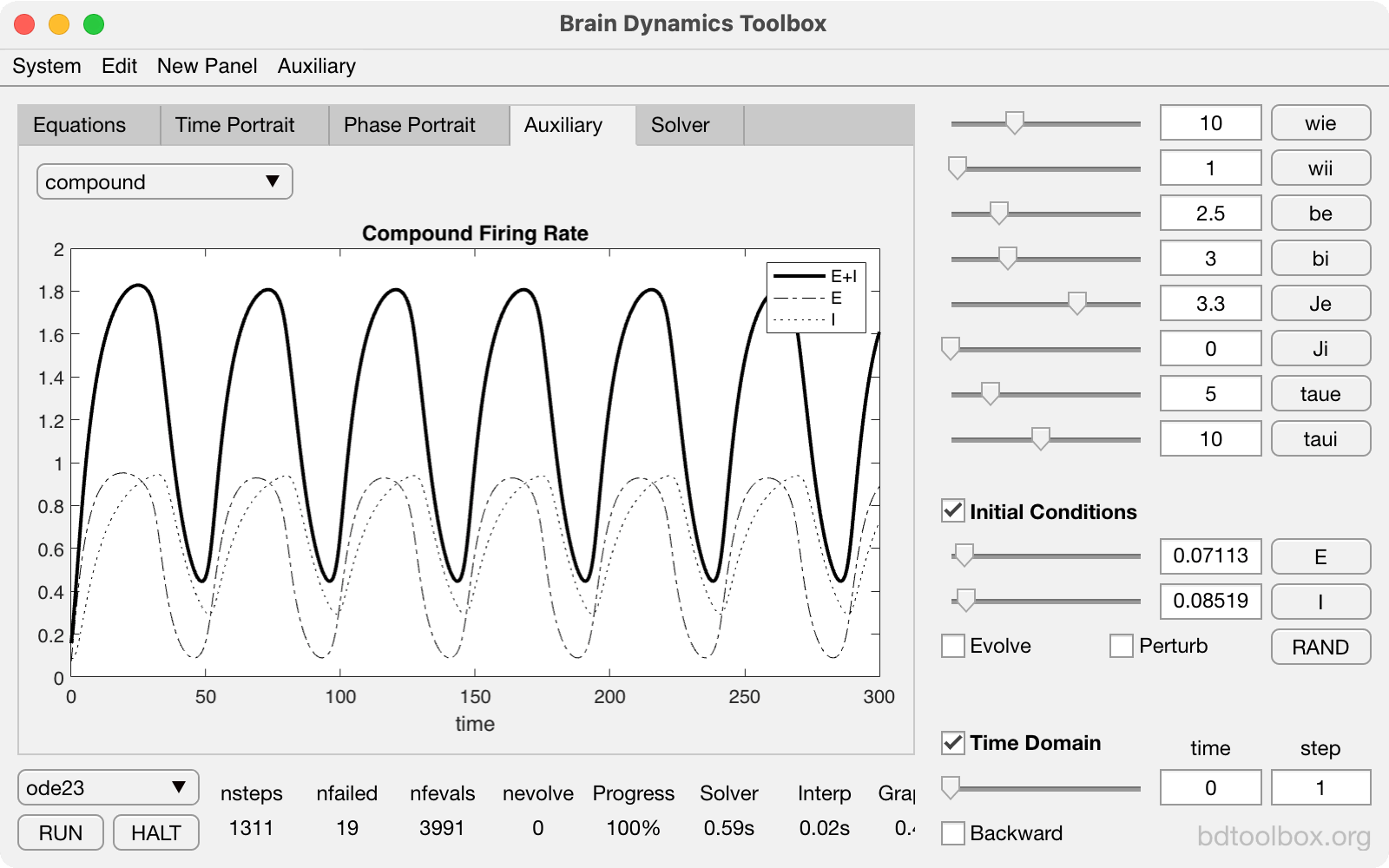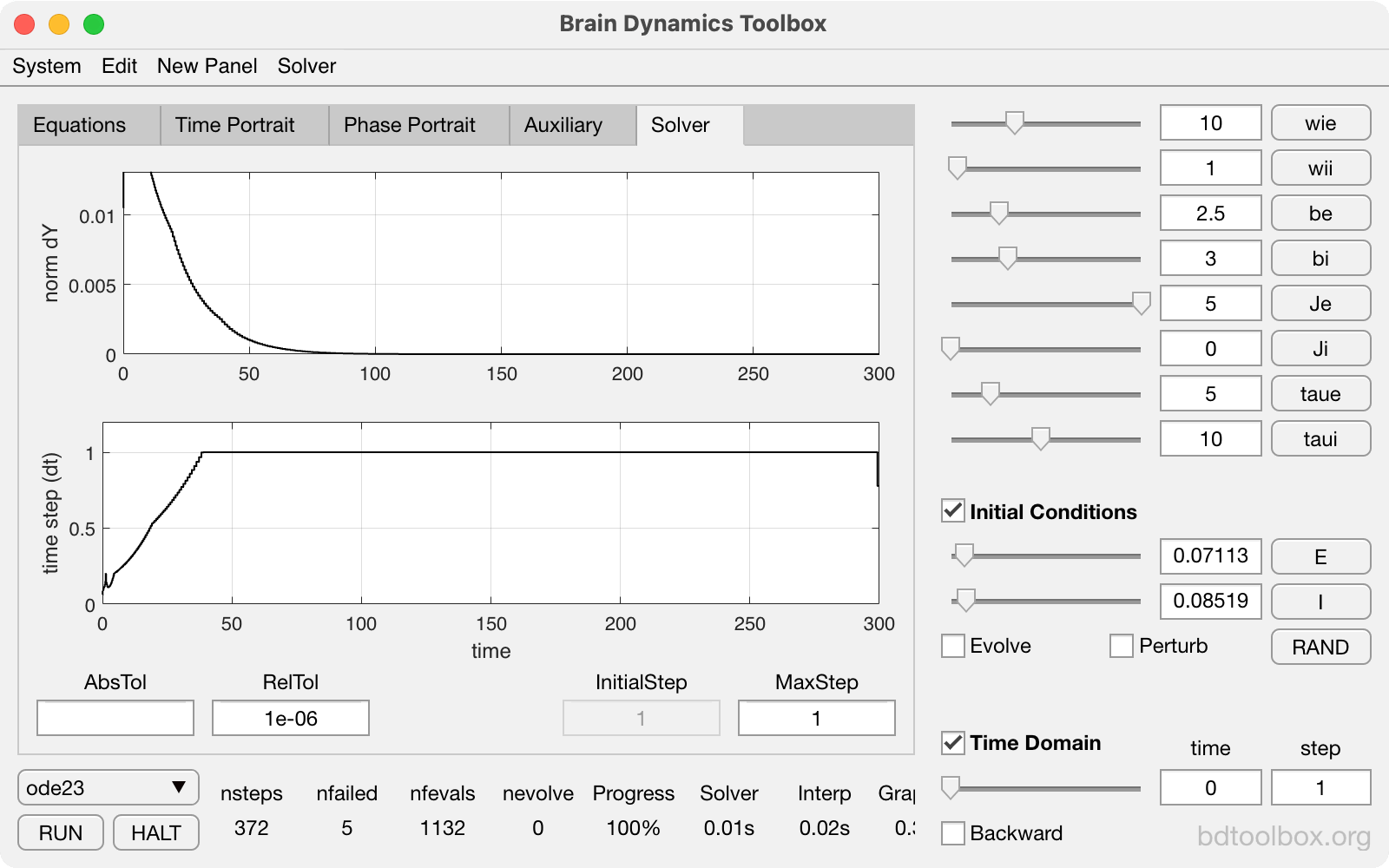	Wilson-Cowan model of reciprocally-coupled excitatory and inhibitory neural populations.
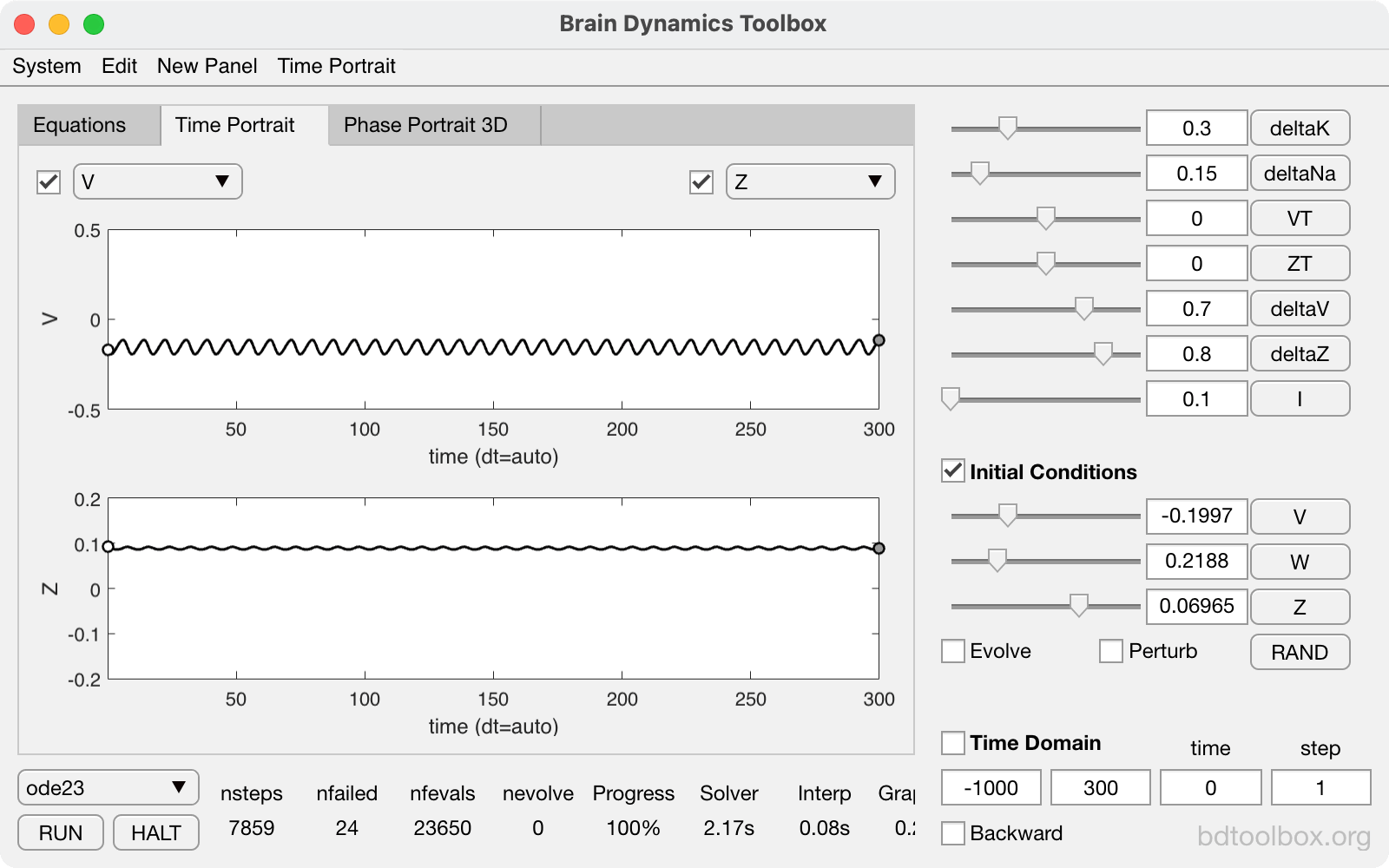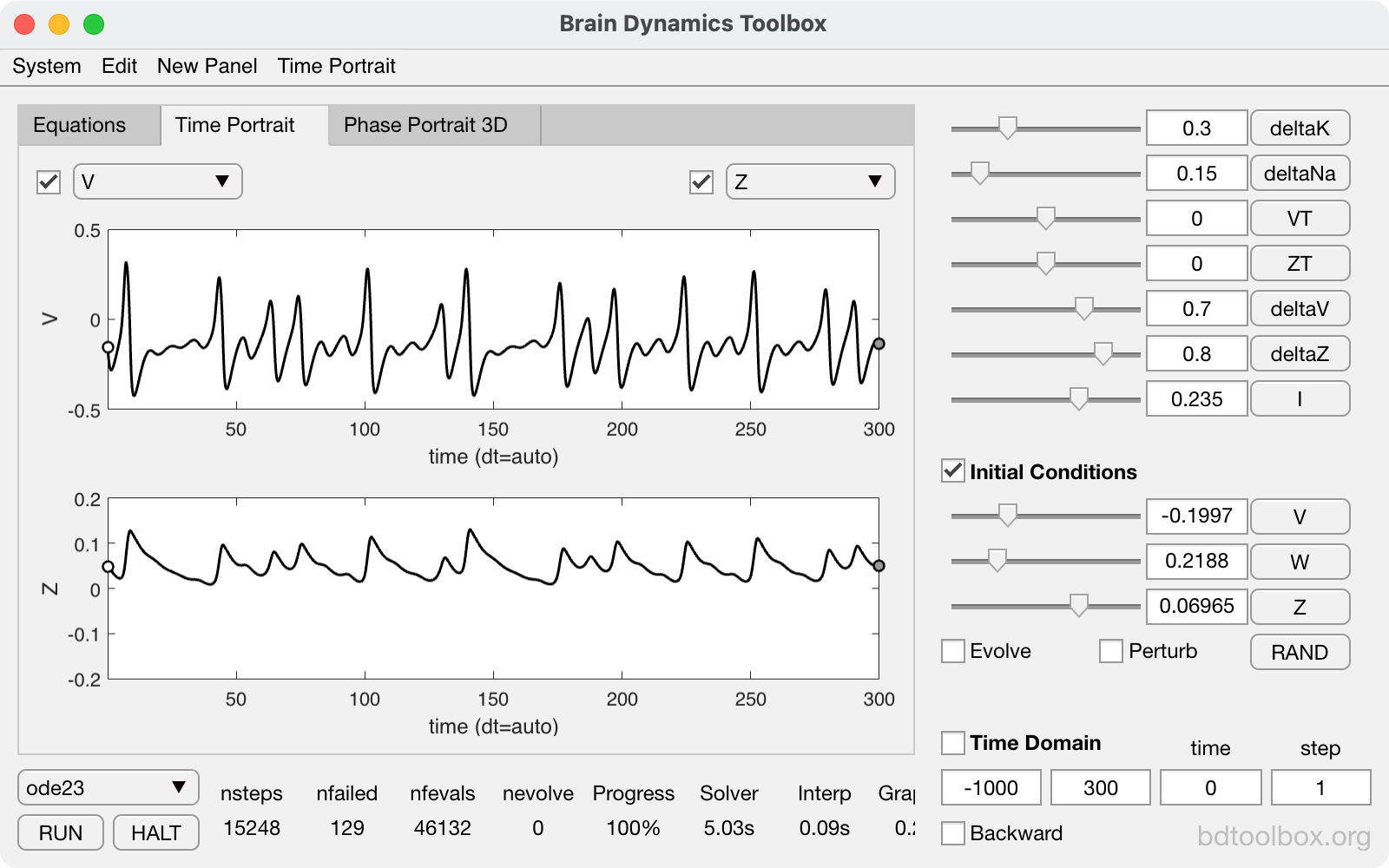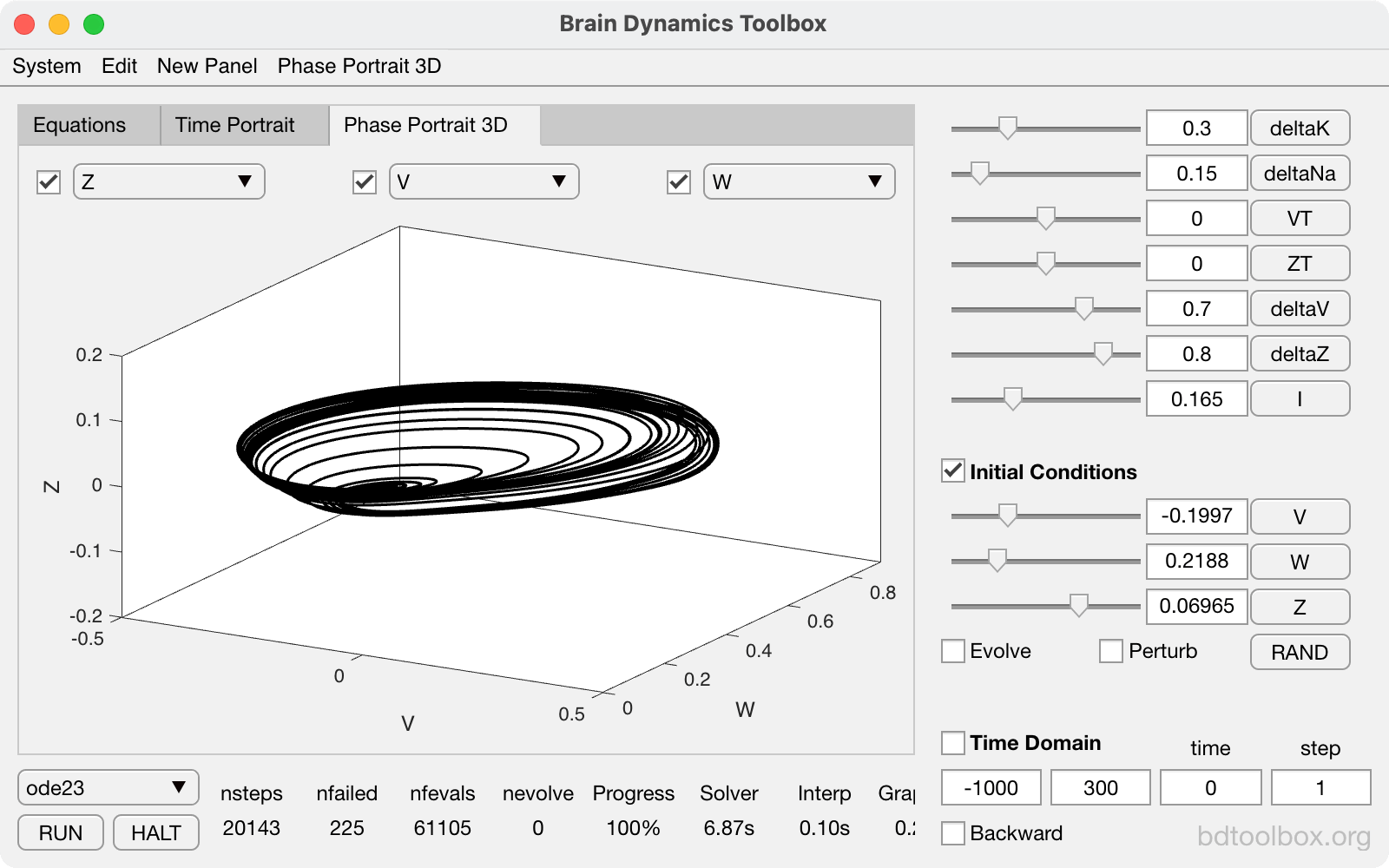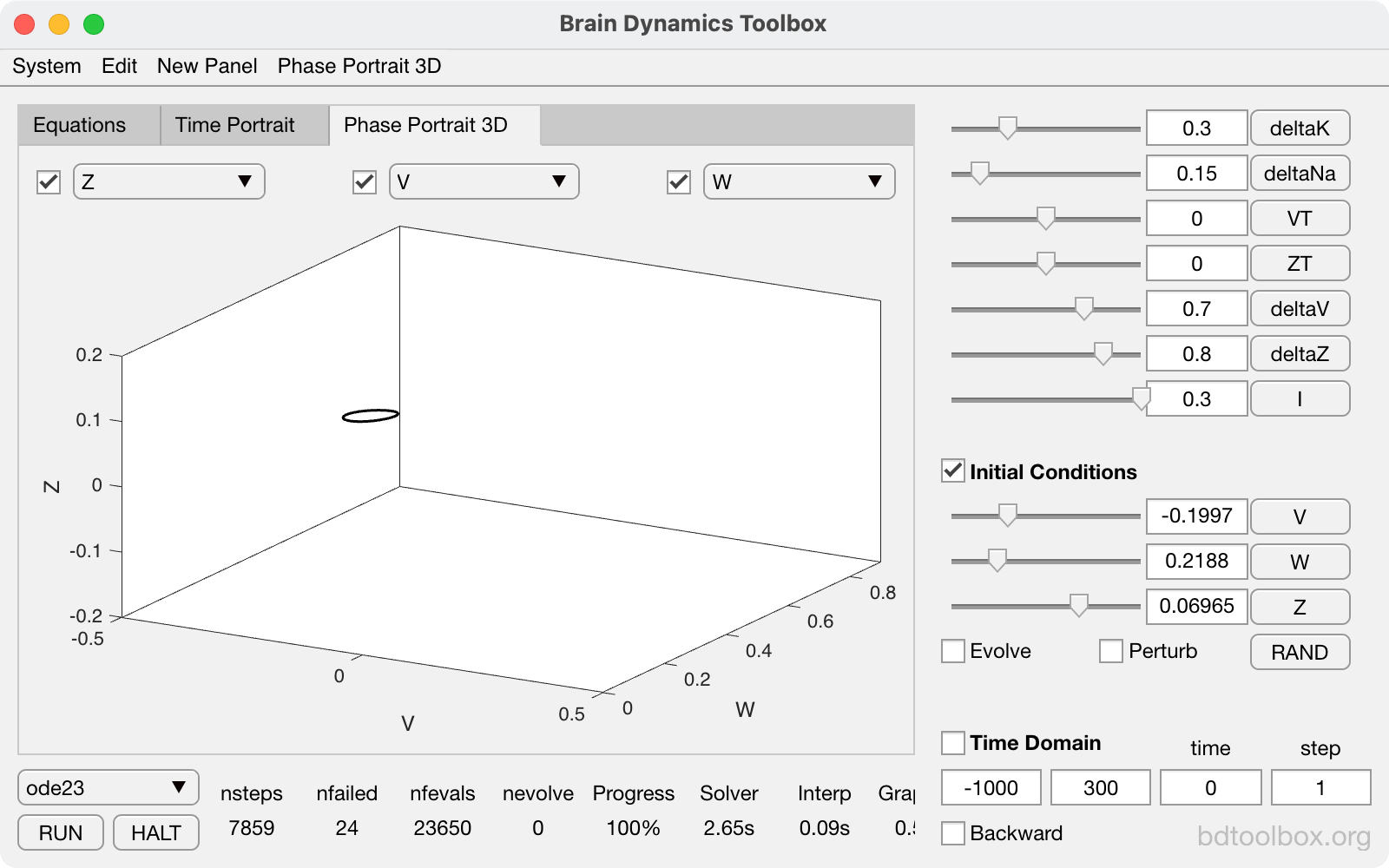	Chaos in the Breakspear-Terry-Friston model.
	Perceptual opponency in the Heitmann-Ermentrout E-I-E model.

---

Spatial Models

	The 2D Wave Equation with reflecting boundary conditions.
	Initiation of spiral rotors in a sheet of FitzHugh-Nagumo neurons.
	Arrhythmogenesis in a heterogeneous sheet of FitzHugh-Nagumo neurons with a tissue boundary.

---

Normal Forms

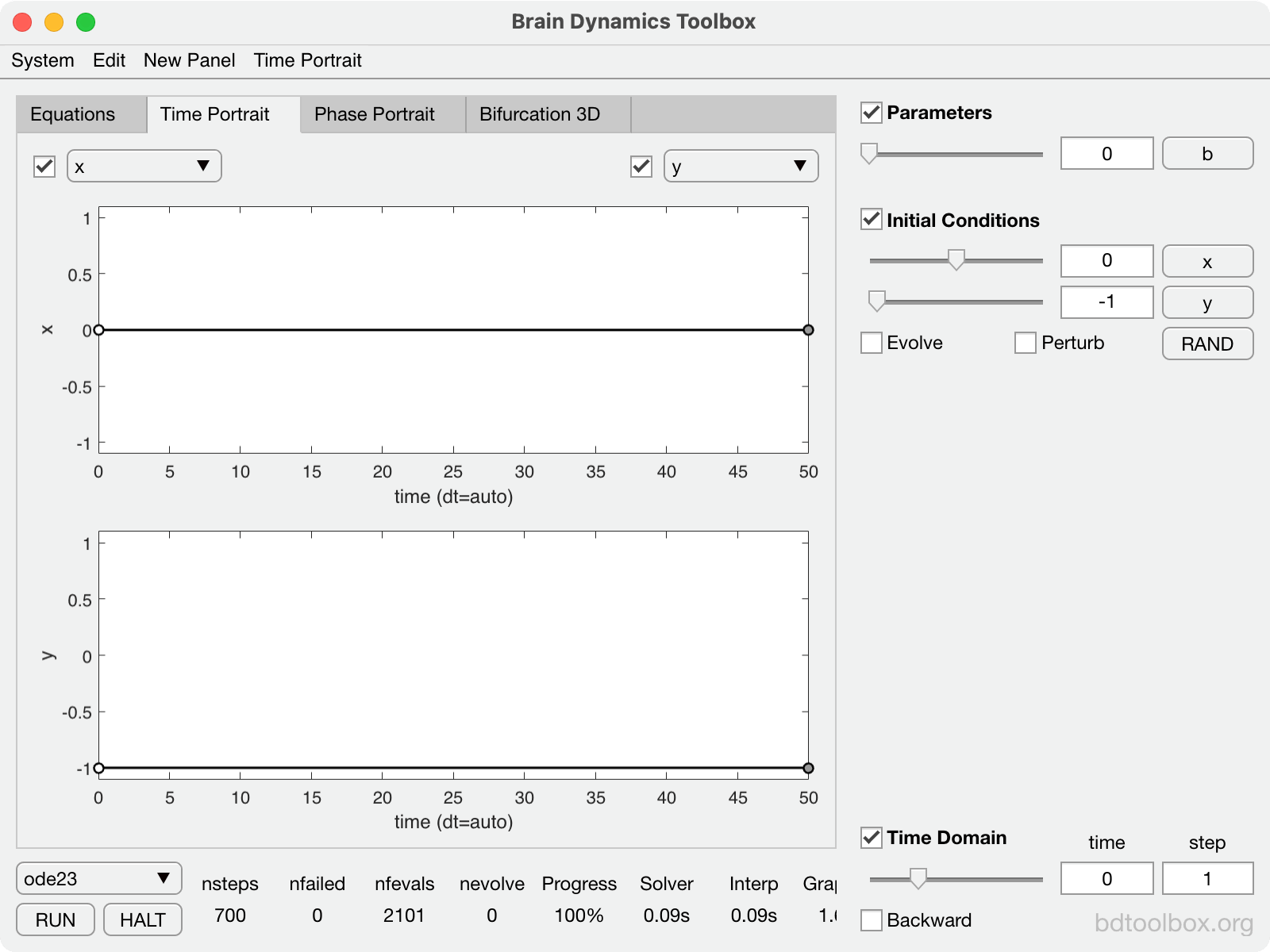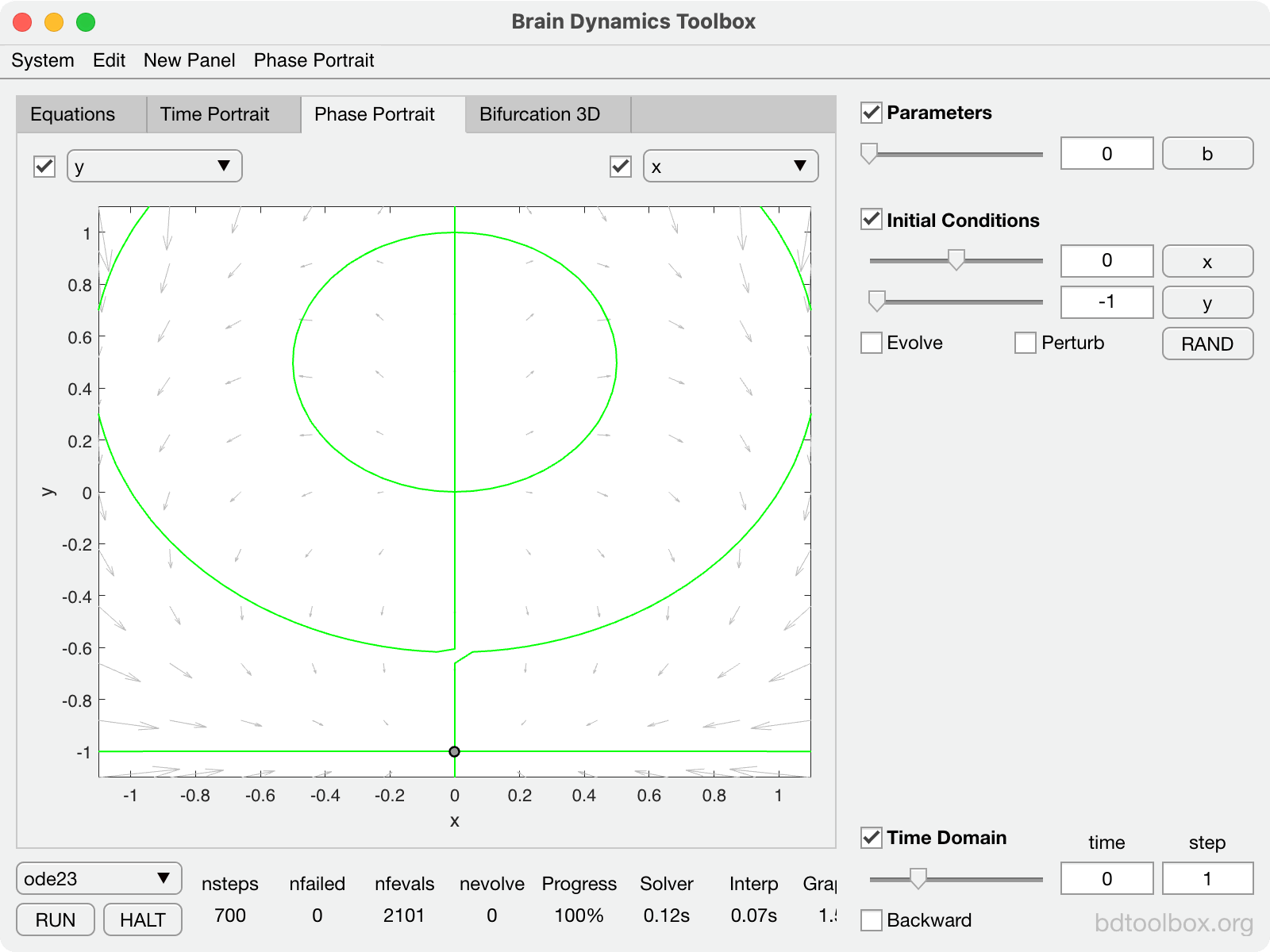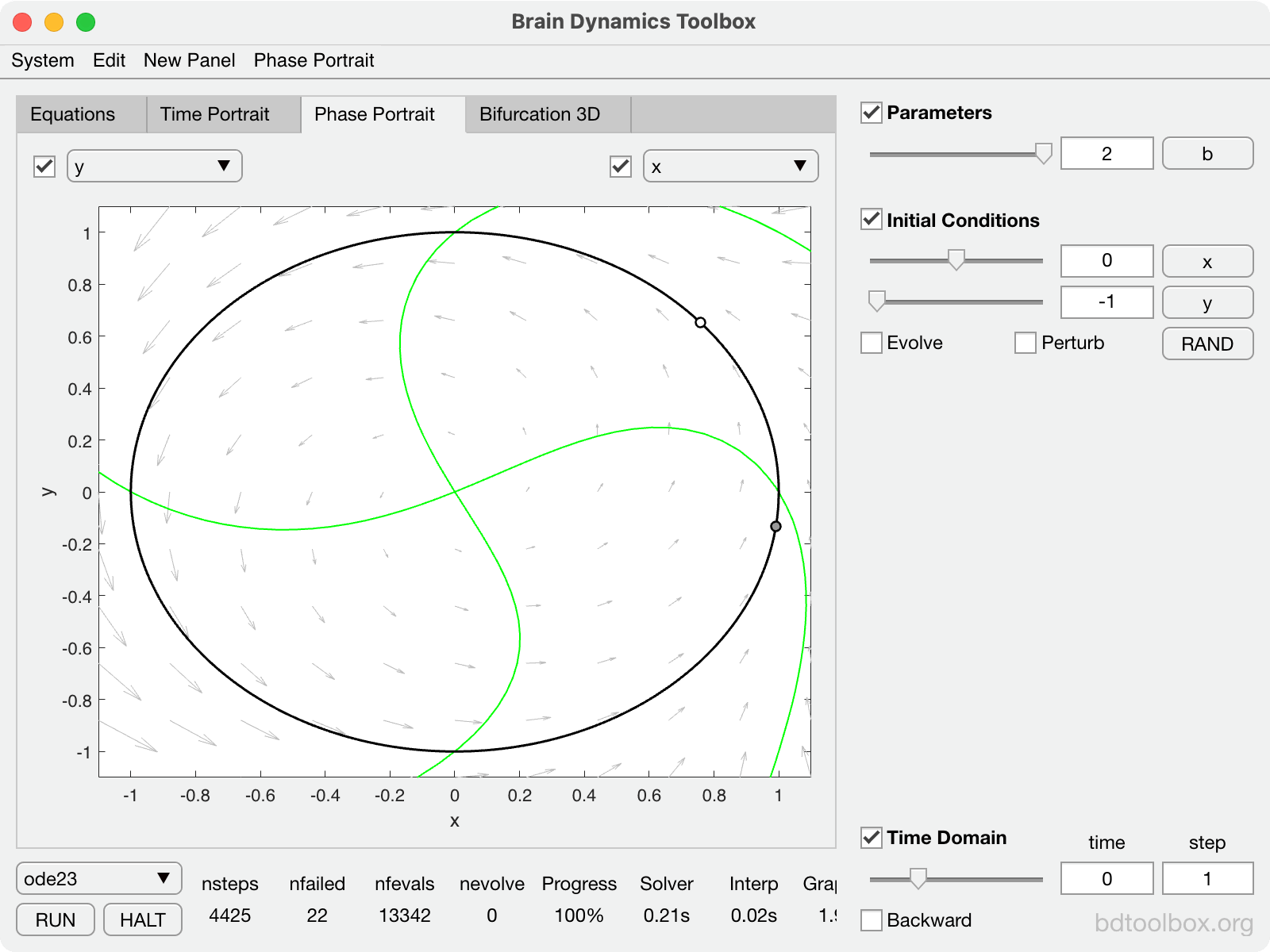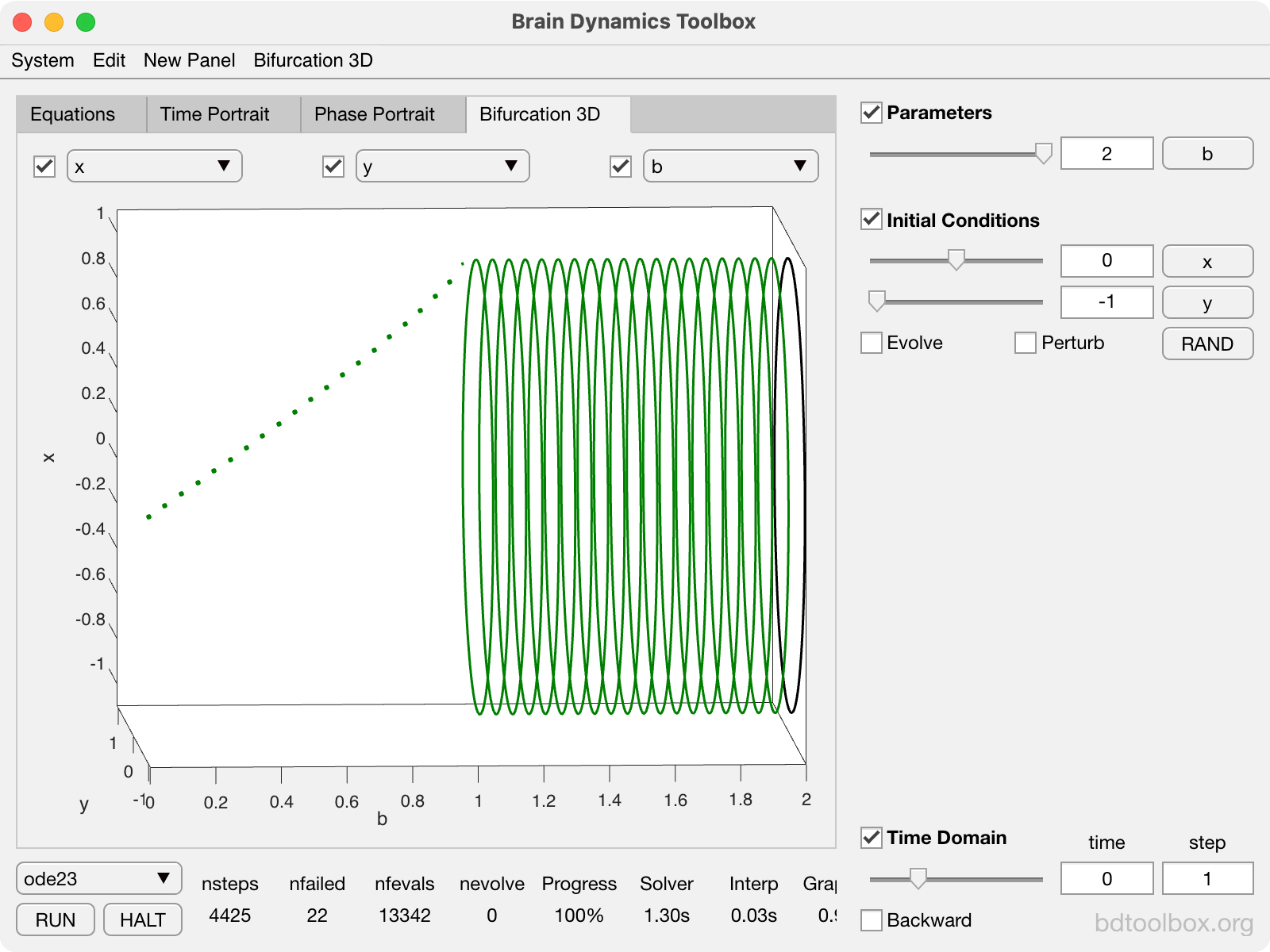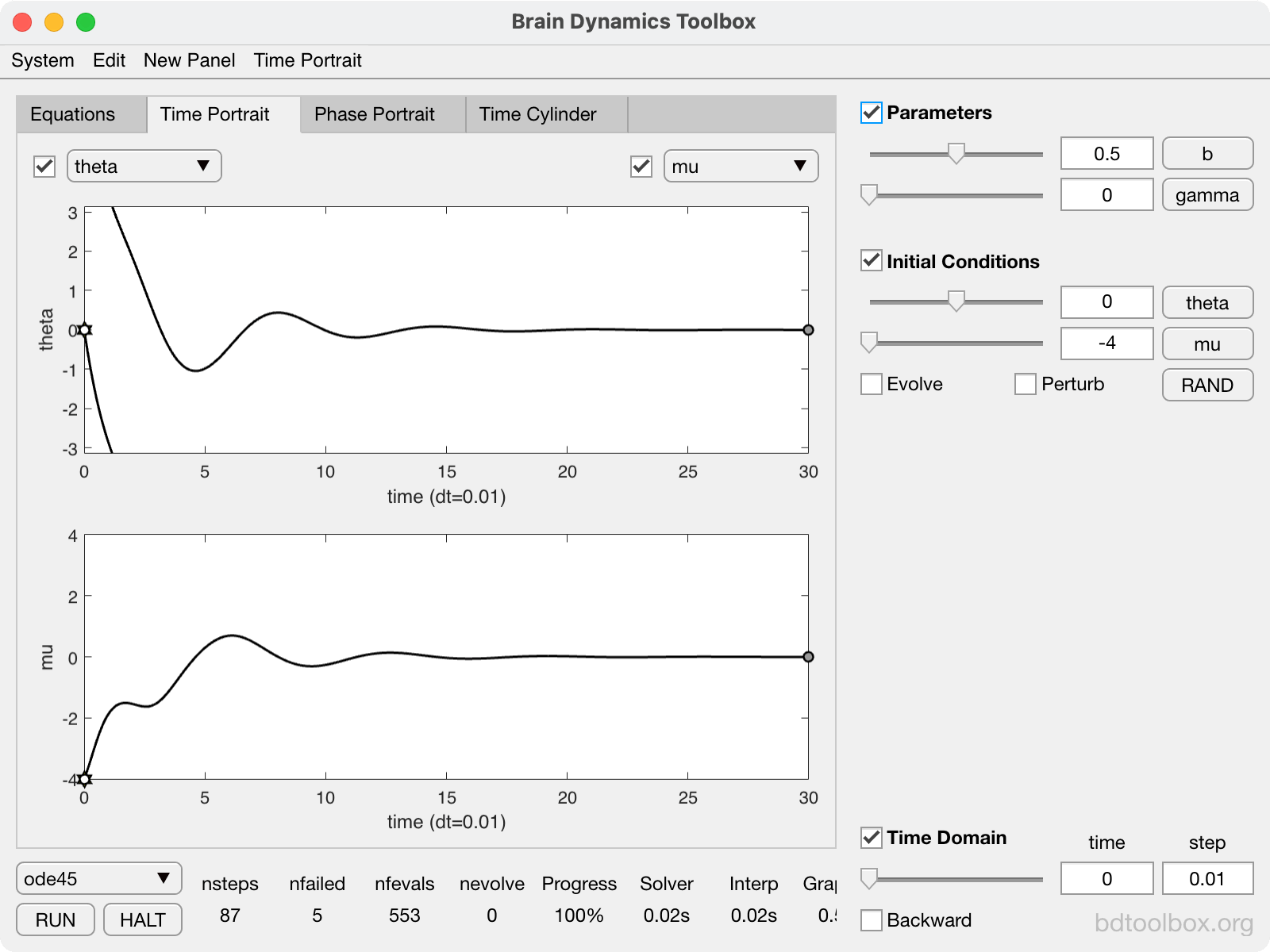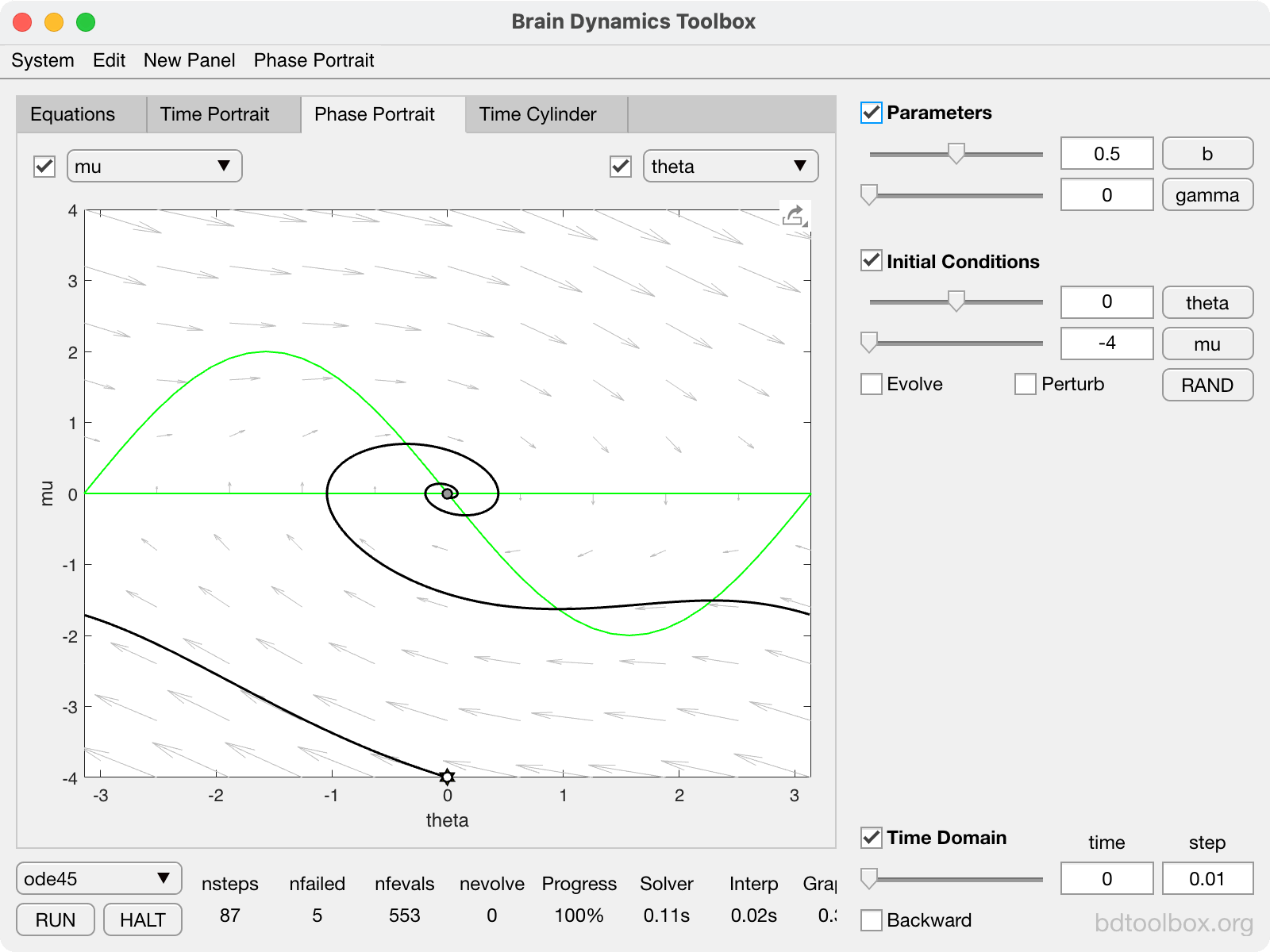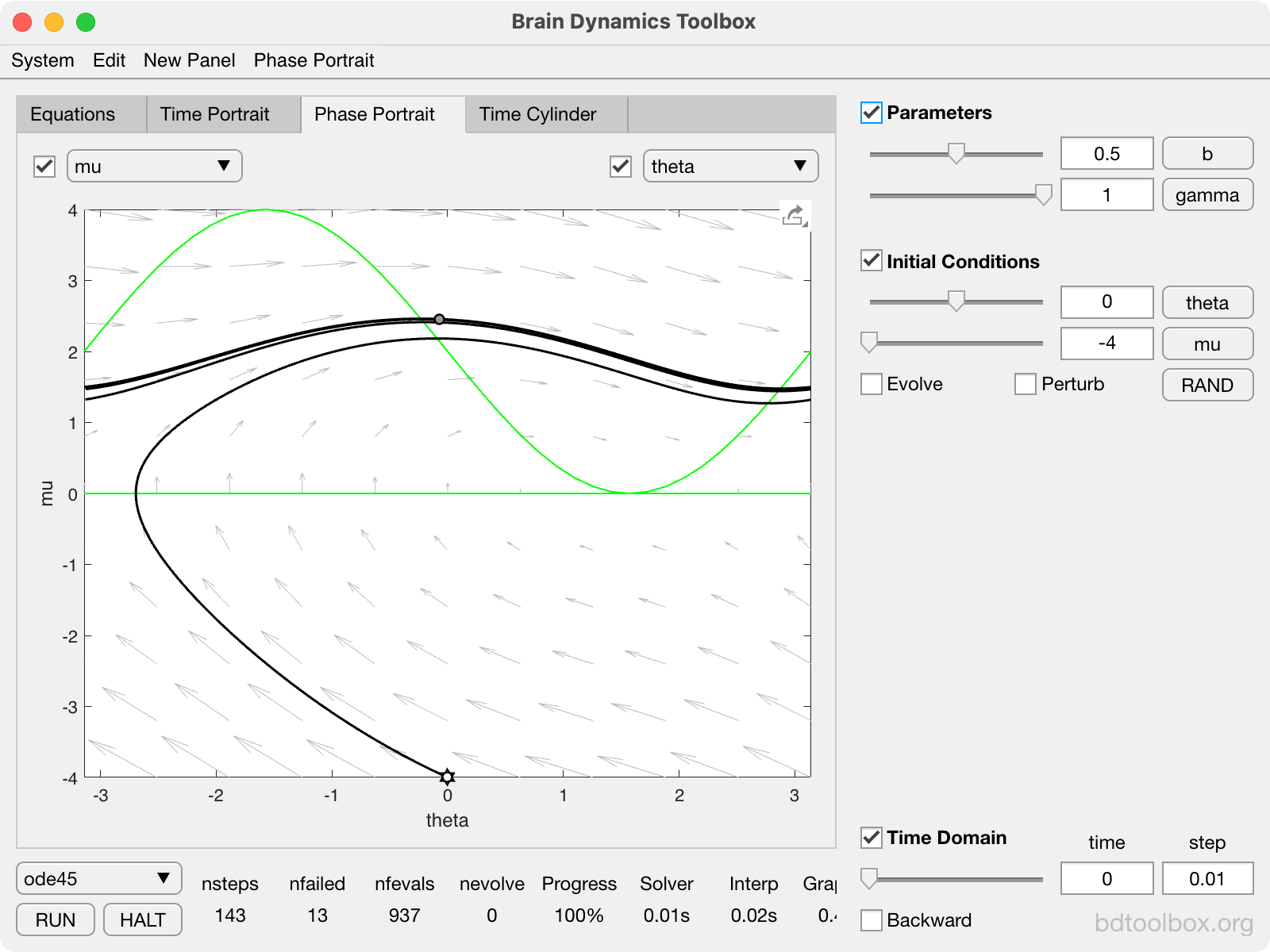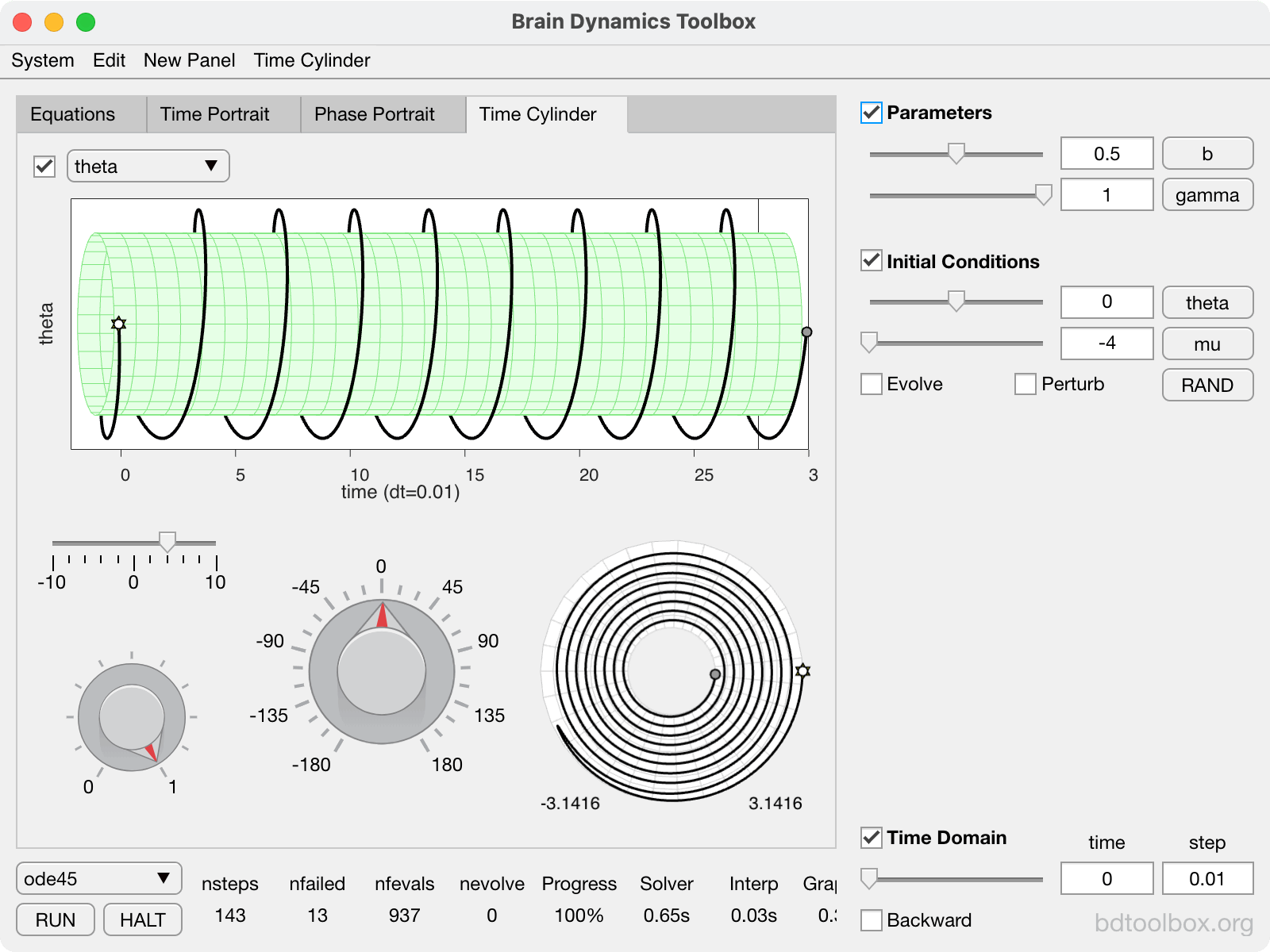
	Normal form of the Saddle-Node bifurcation on a Limit Cycle. The basis of Type-1 neural excitability.
	Normal form of the Supercritical Hopf bifurcation. The basis of Type-2 neural excitability.

---

Classics

	Determistic chaos in the Lorenz Attractor.
	The damped-and-driven pendulum.
	The Van Der Pol relaxation oscillator.
	The Lotka-Volterra predator-prey equations.
	Arithmetic Brownian Motion. Drift and diffusion.
	Geometric Brownian Motion. Multiplicative noise. Mathematical finance.

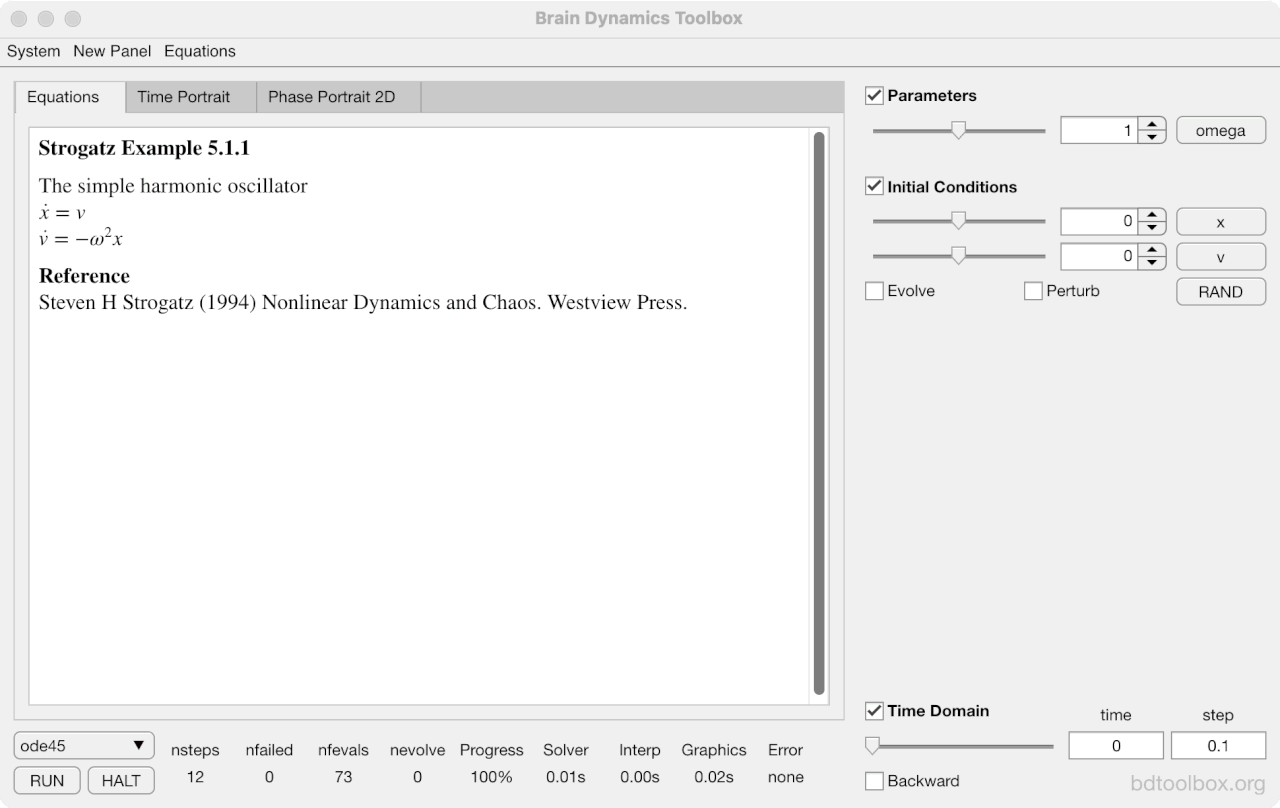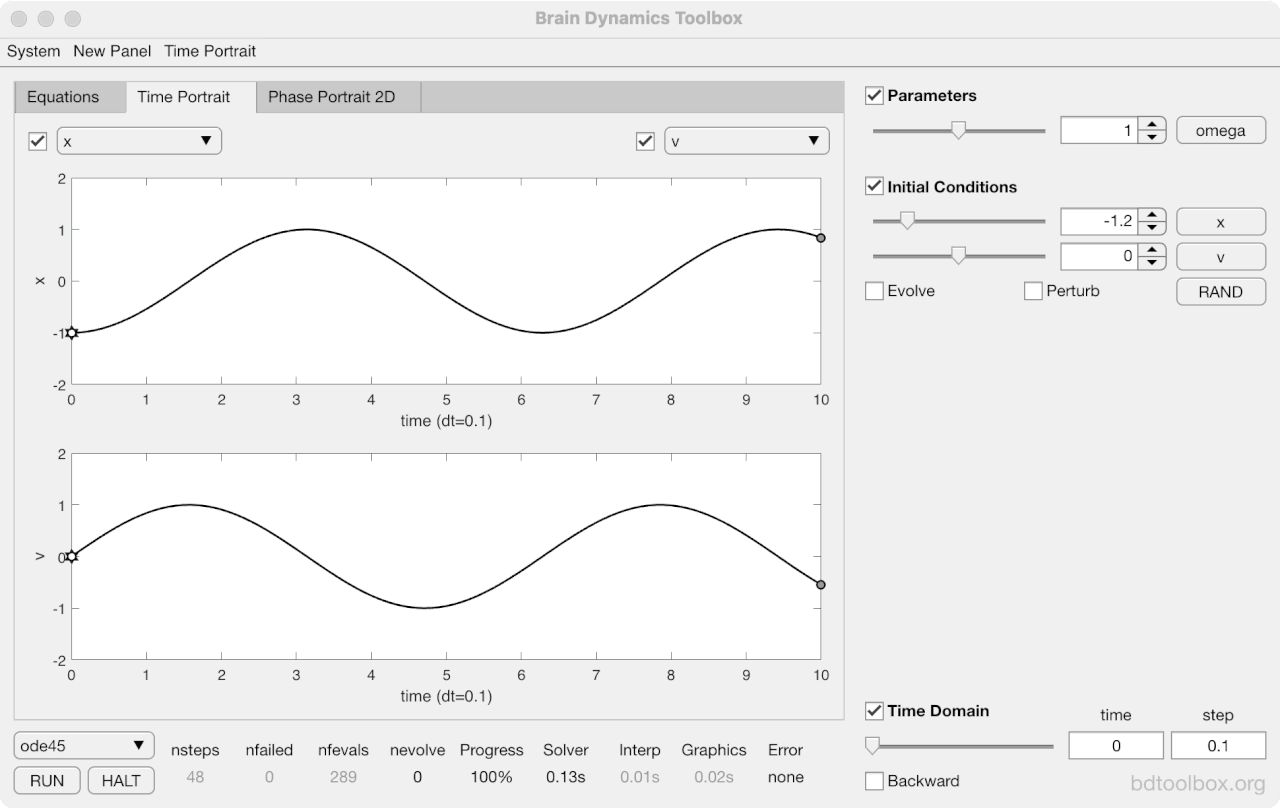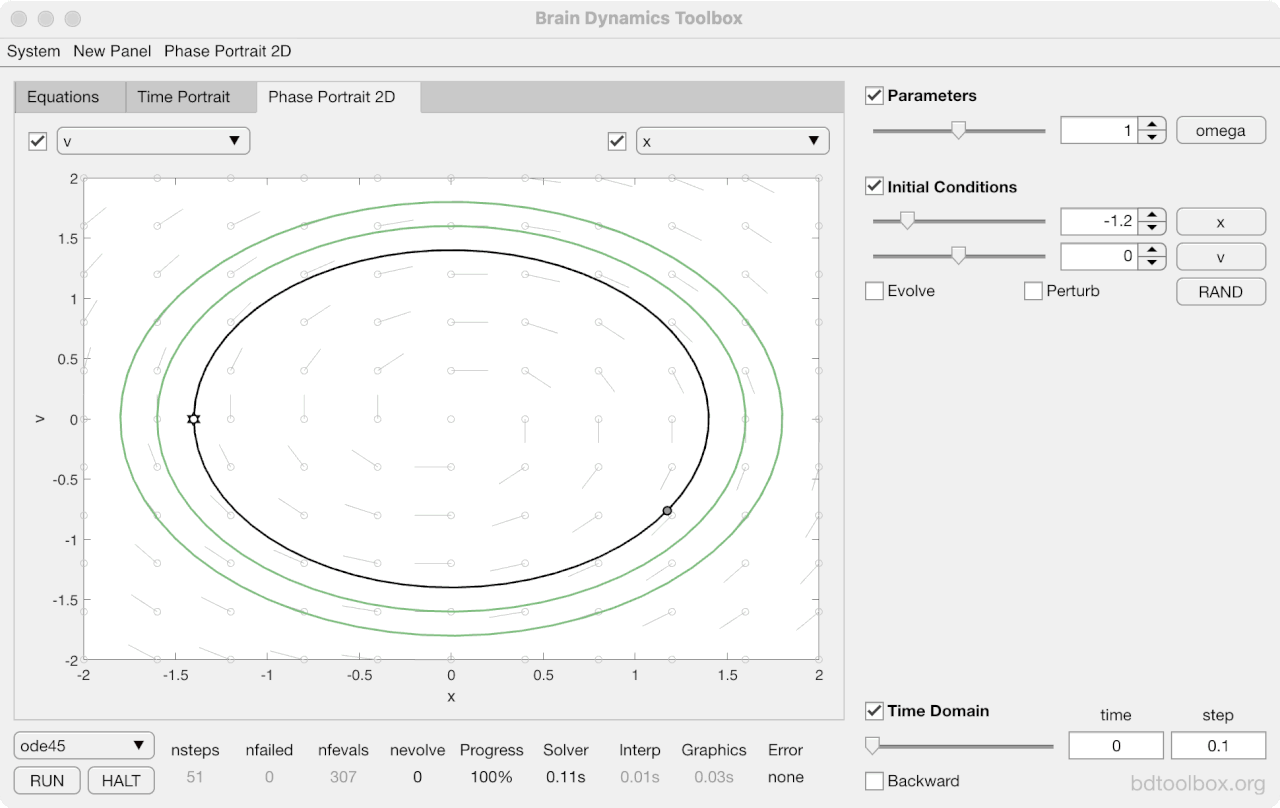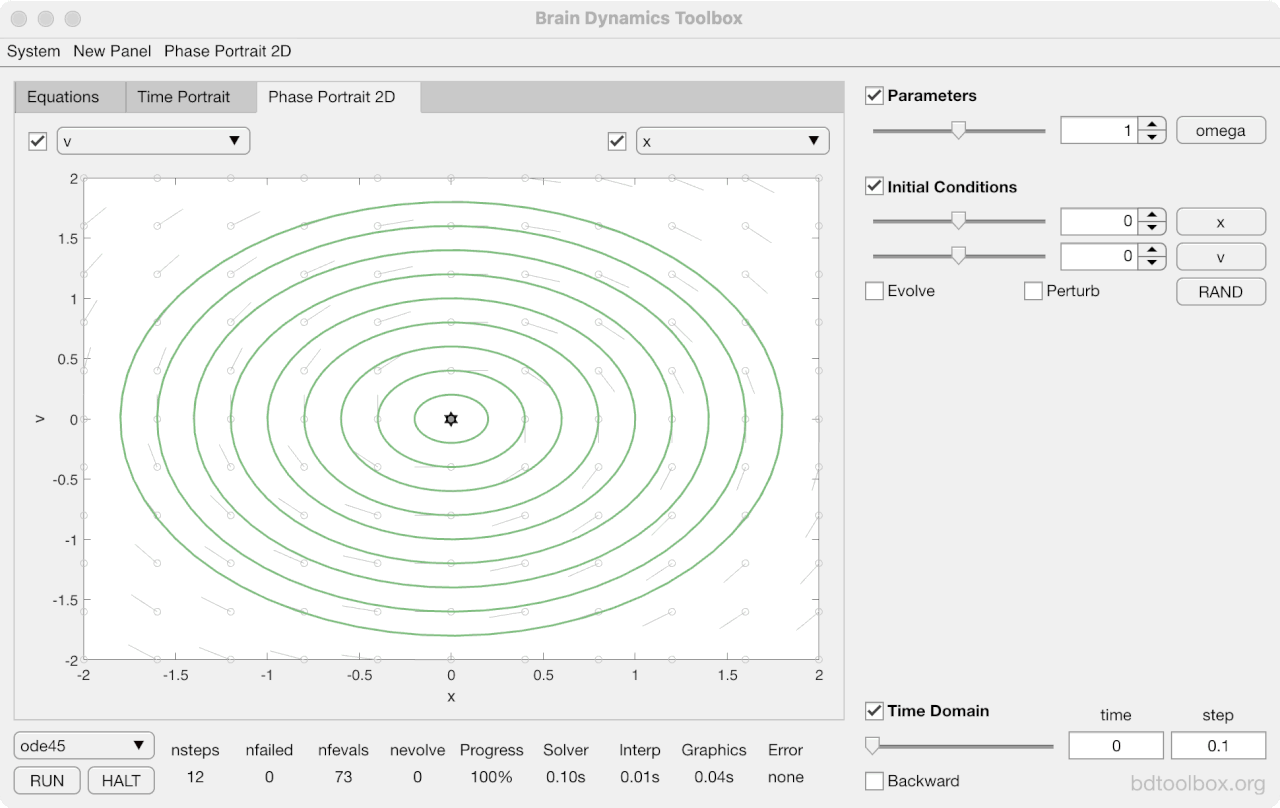
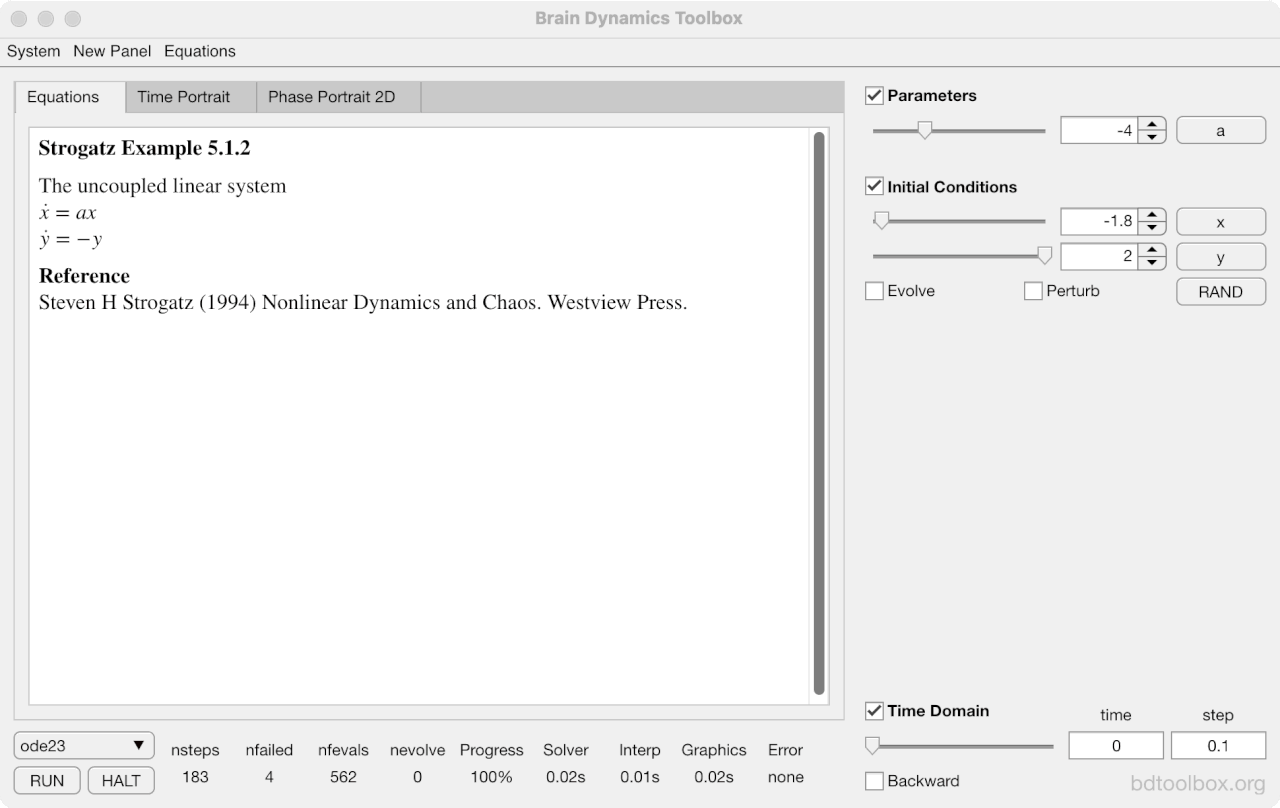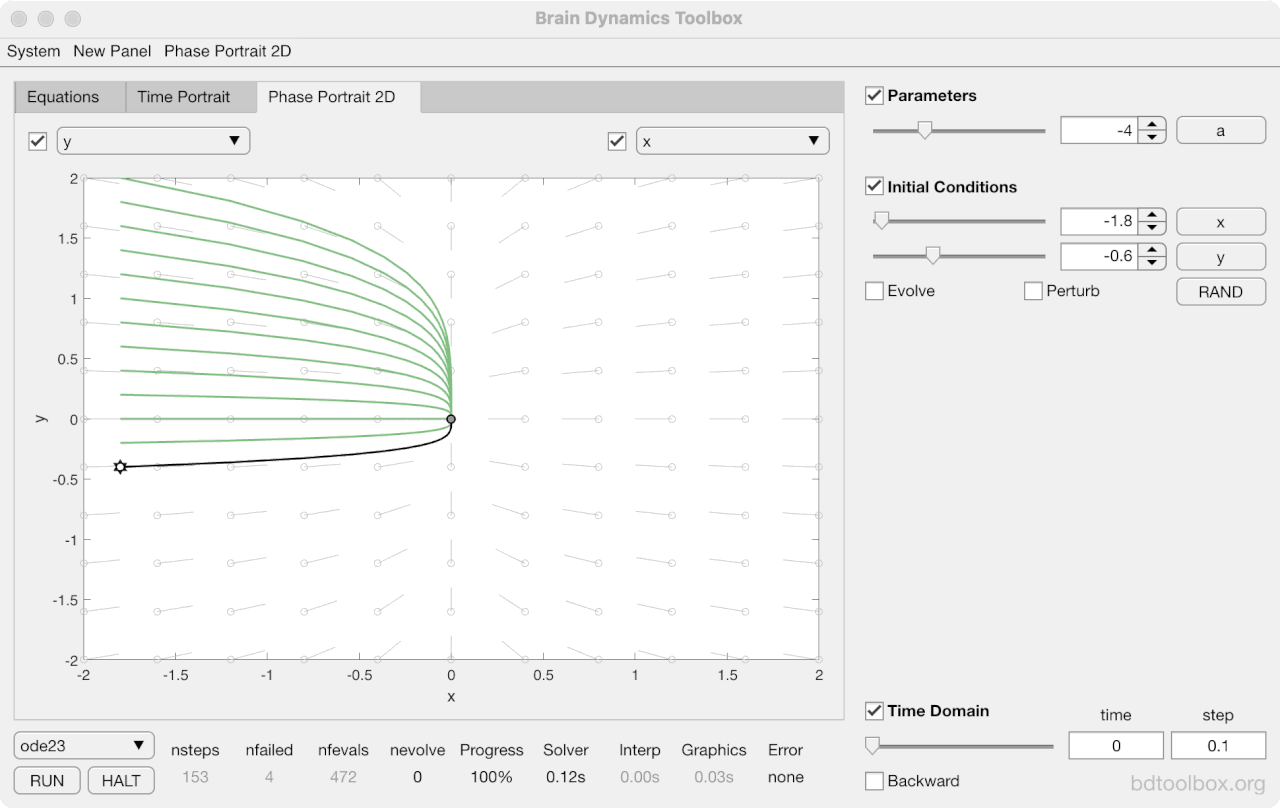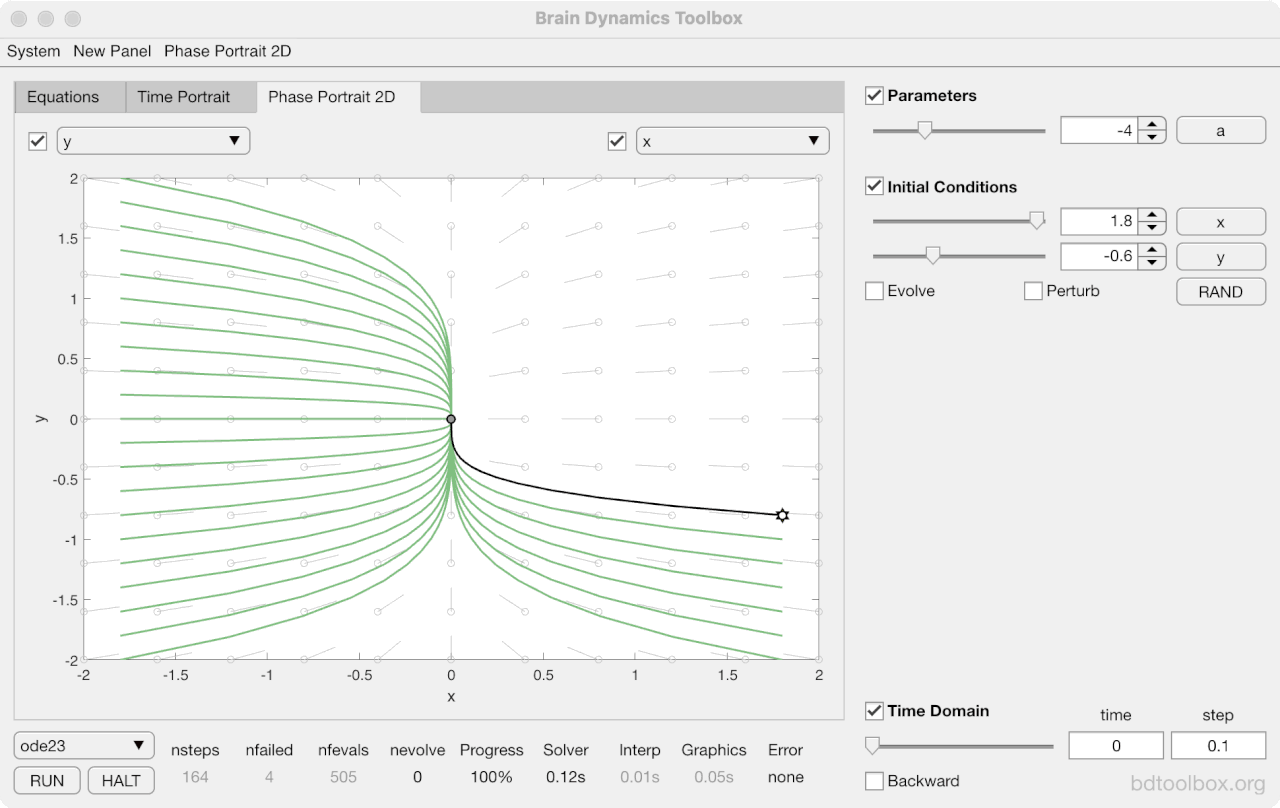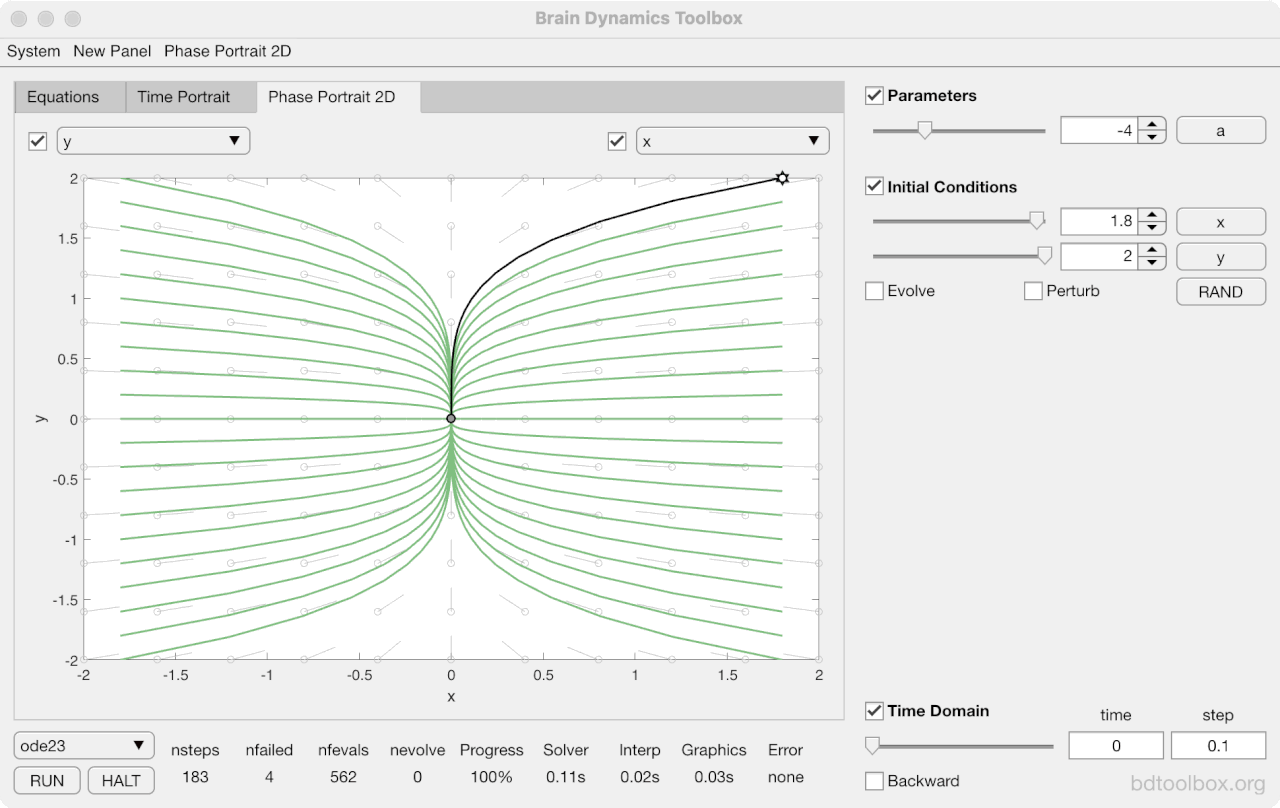
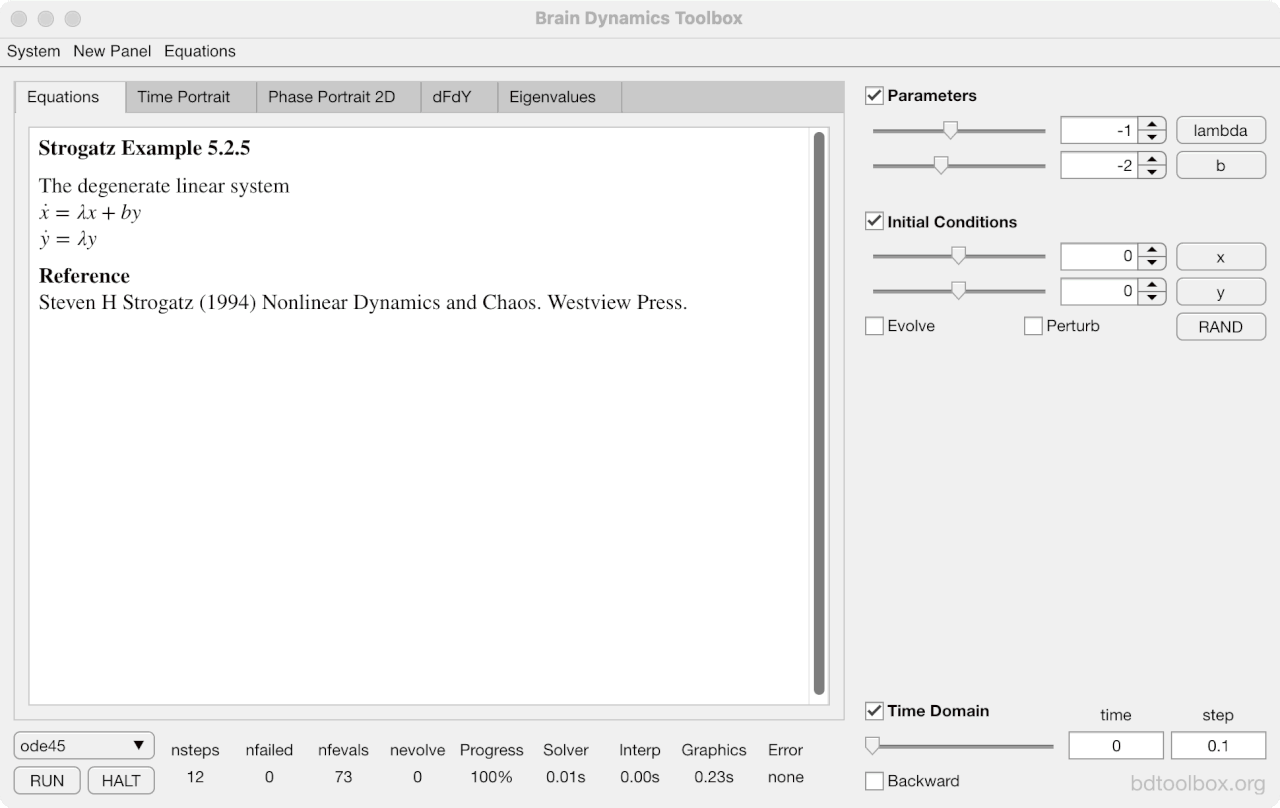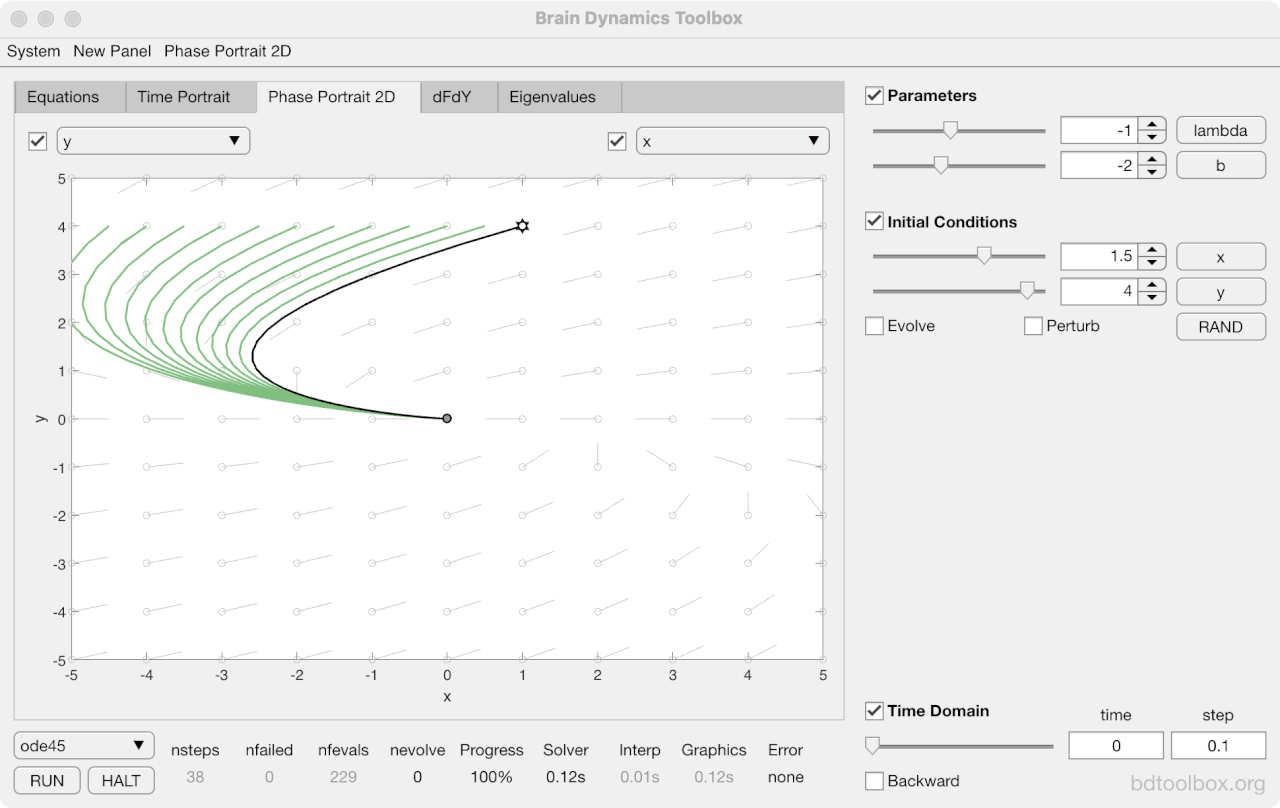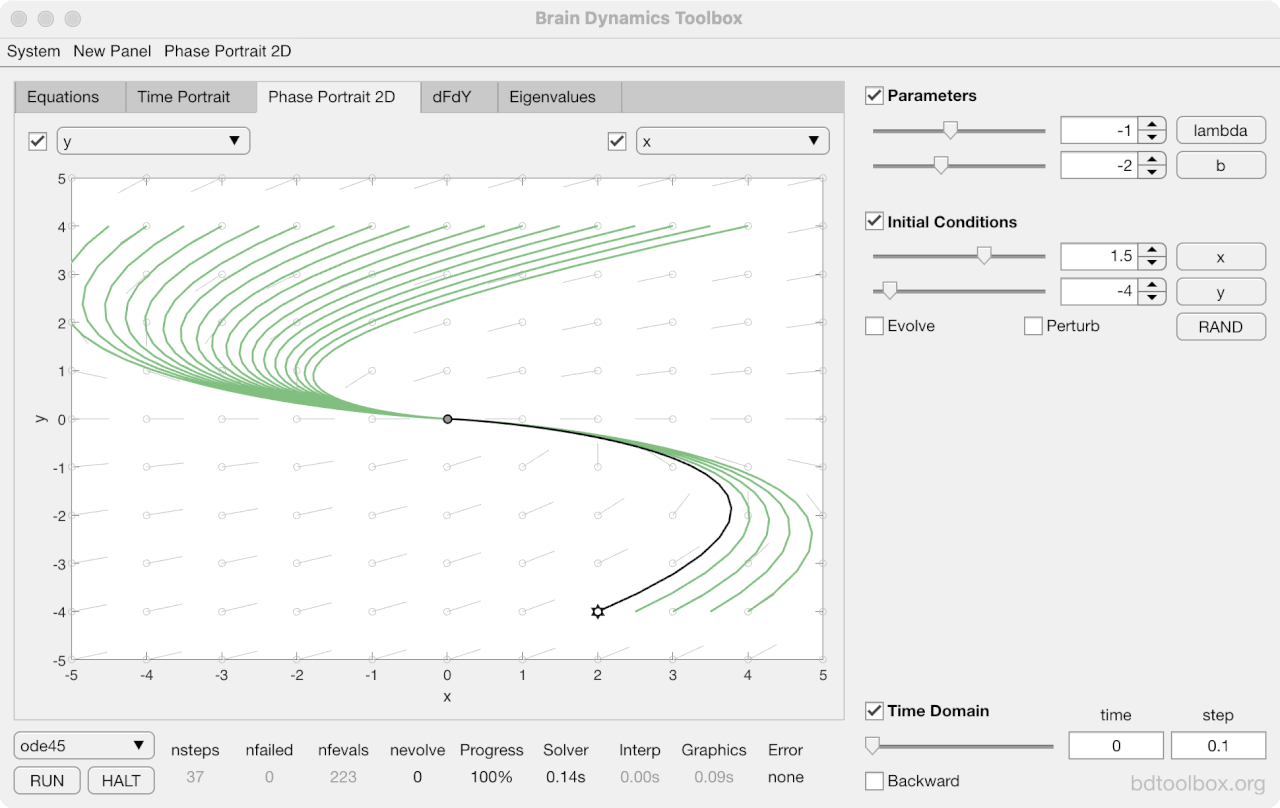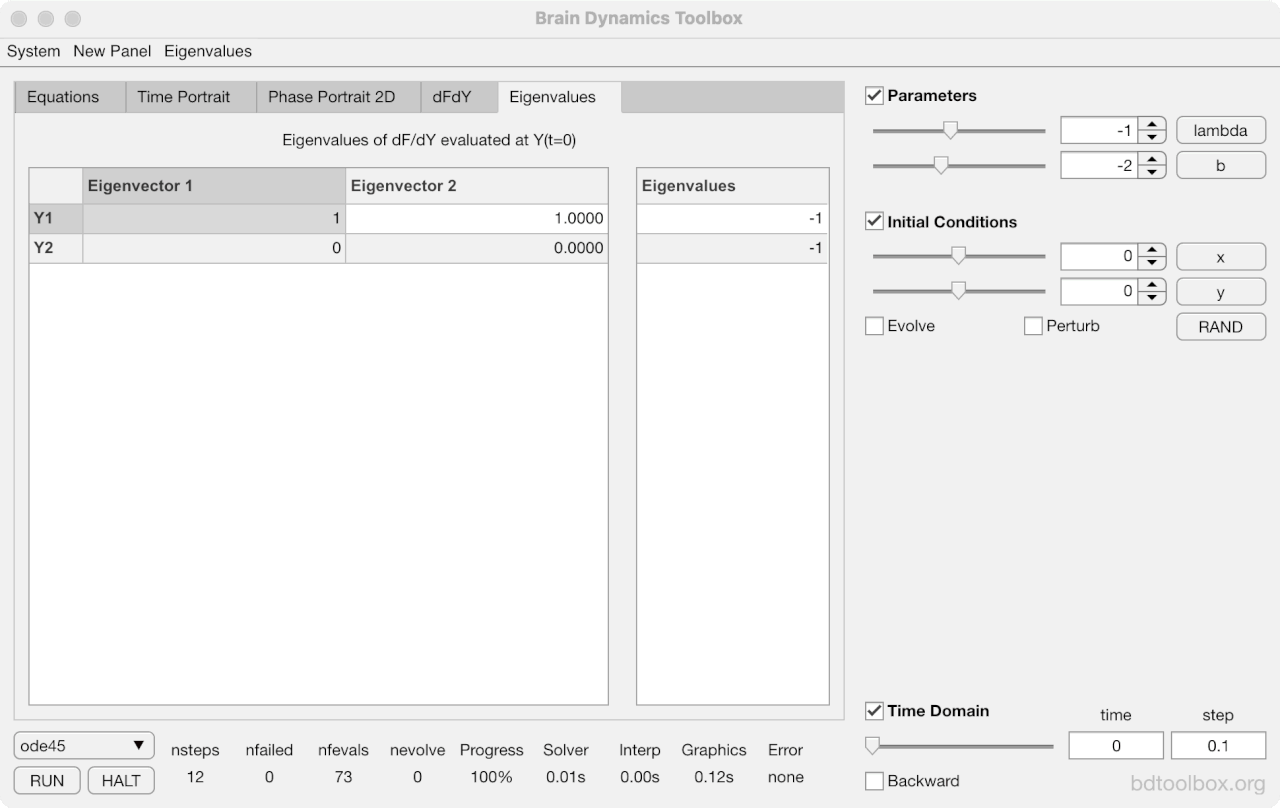
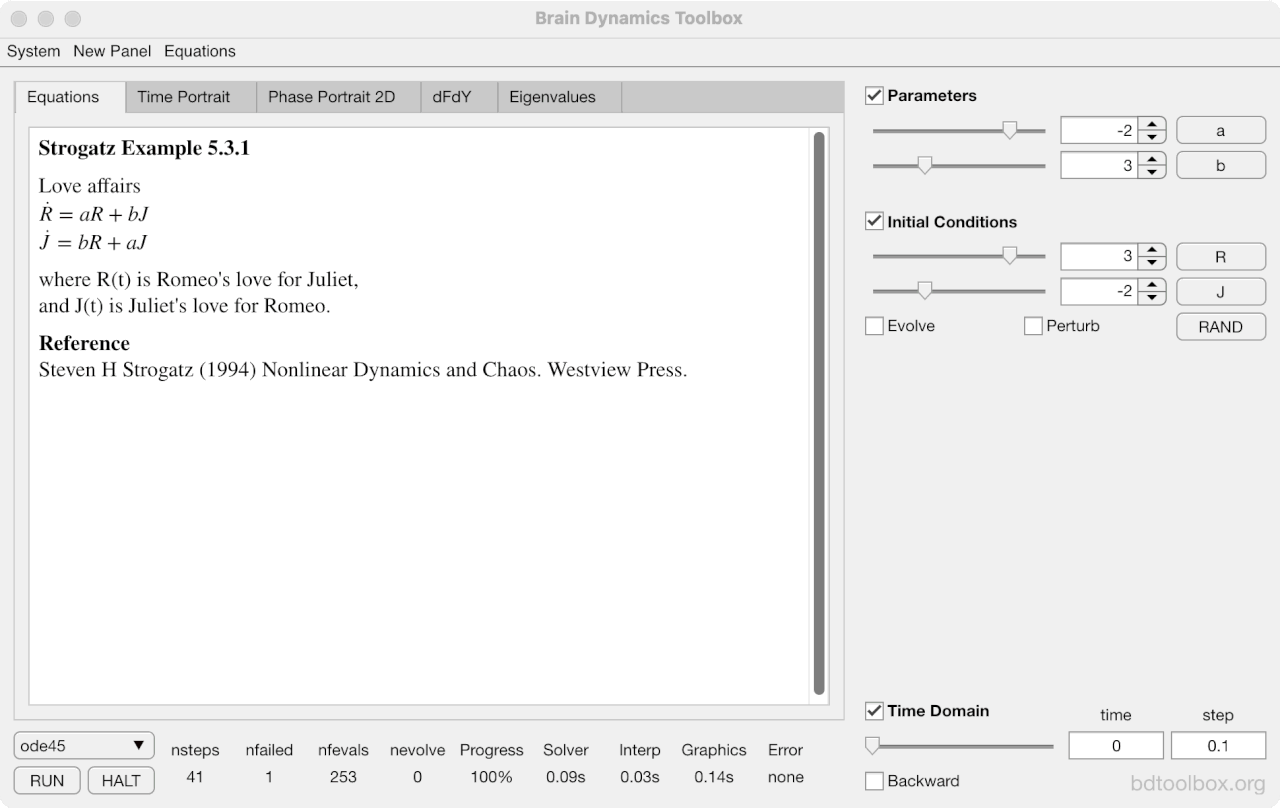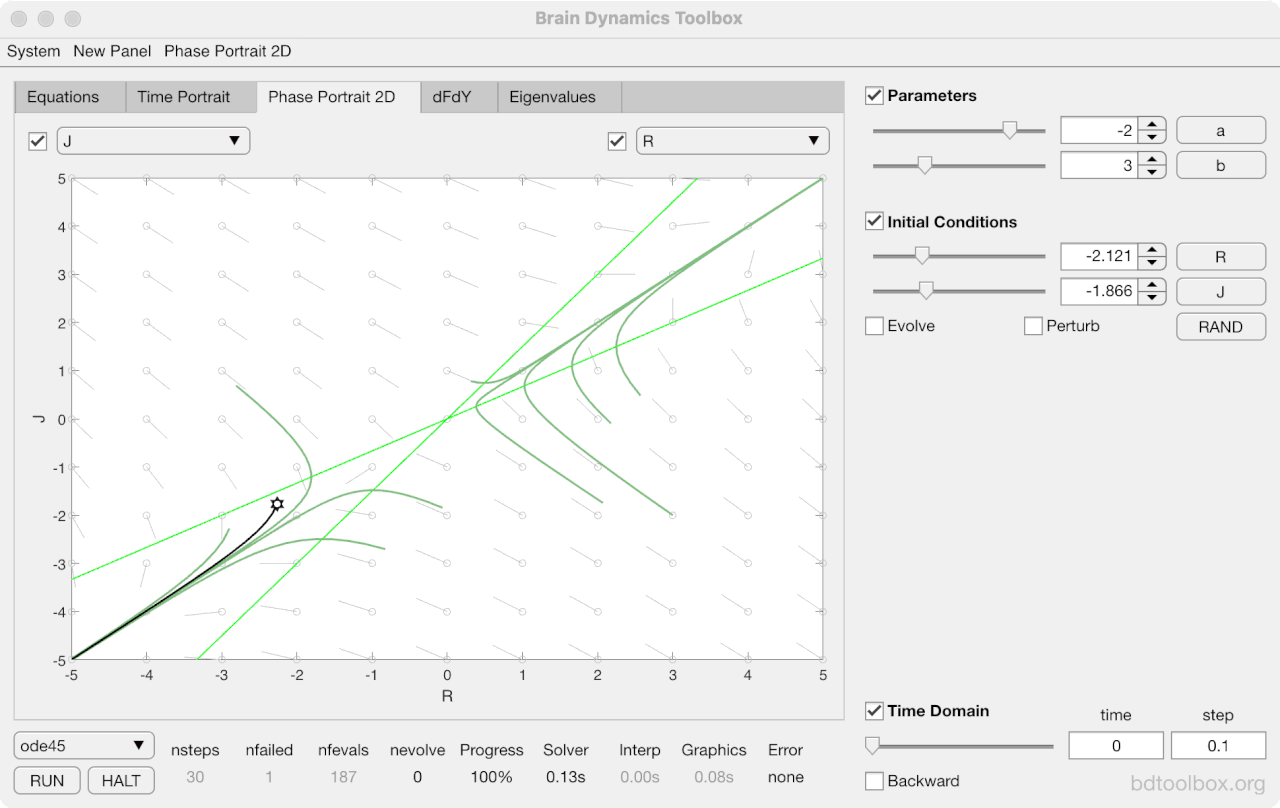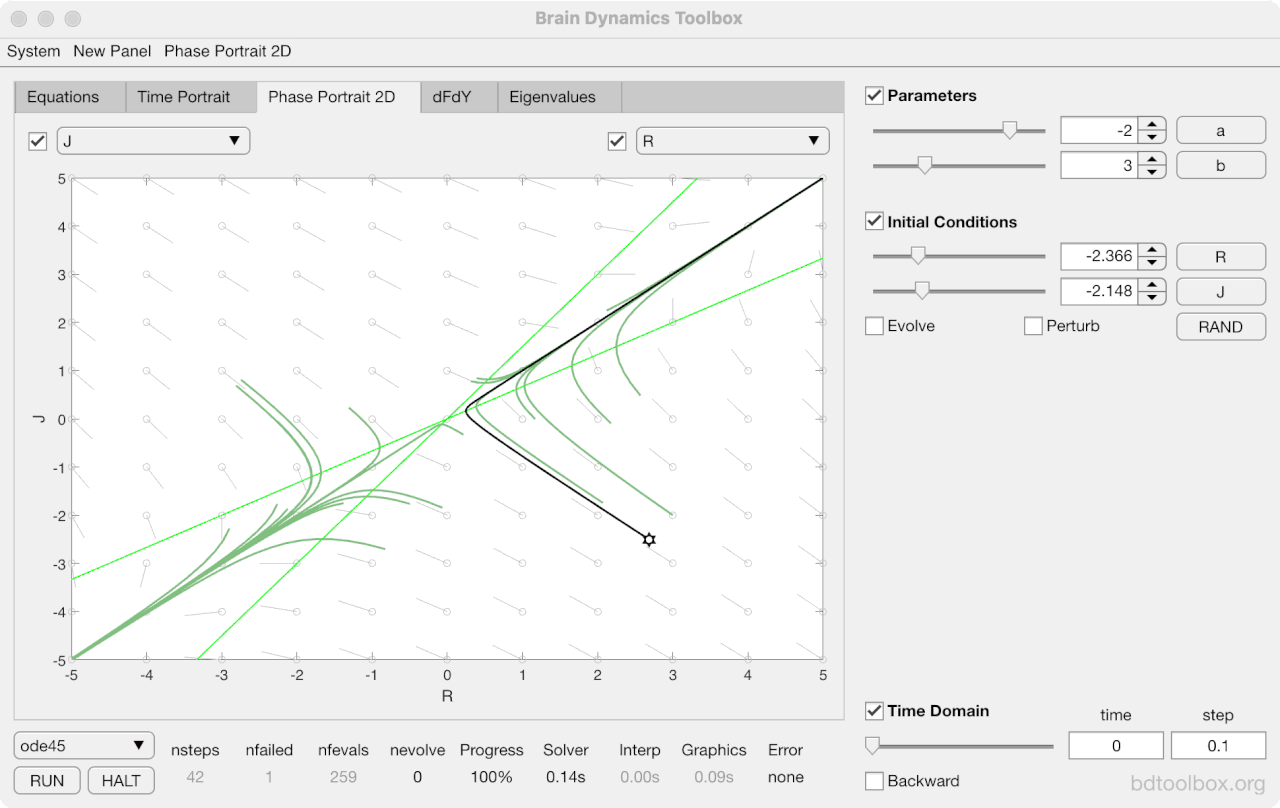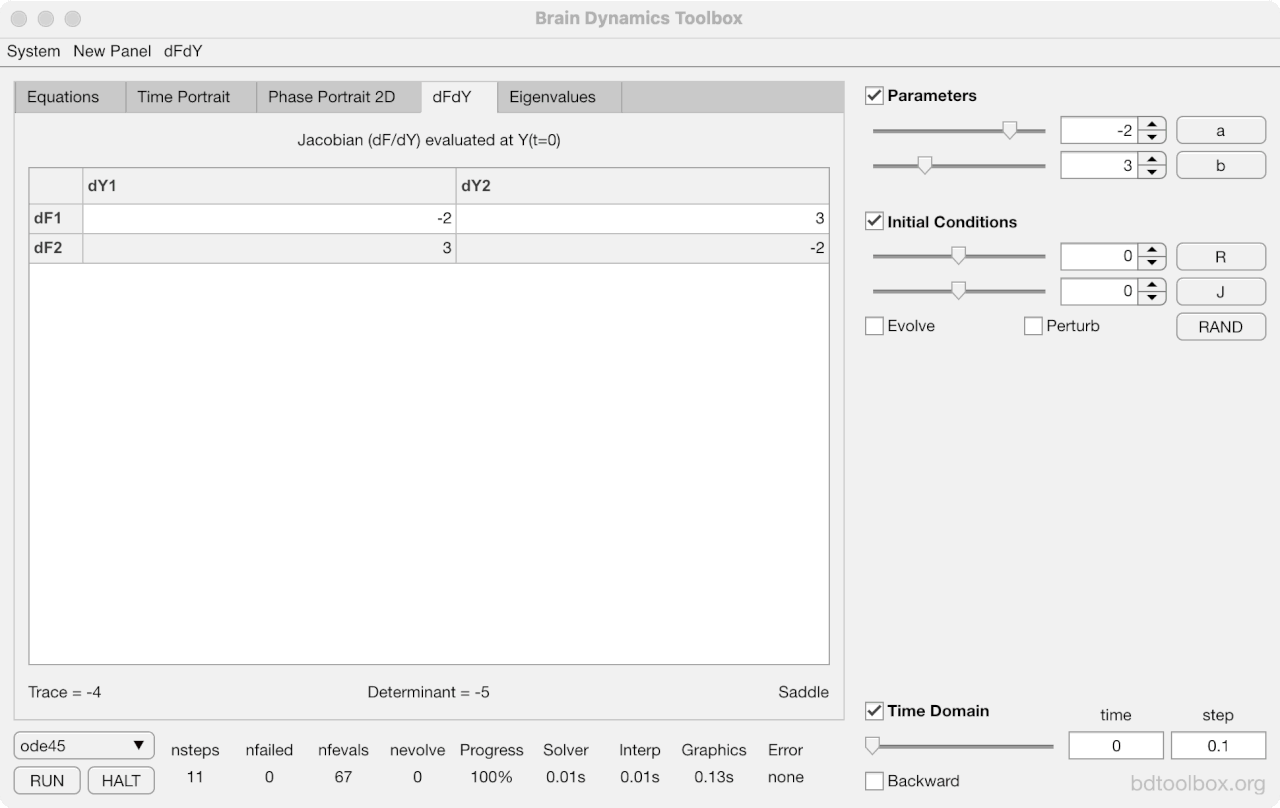
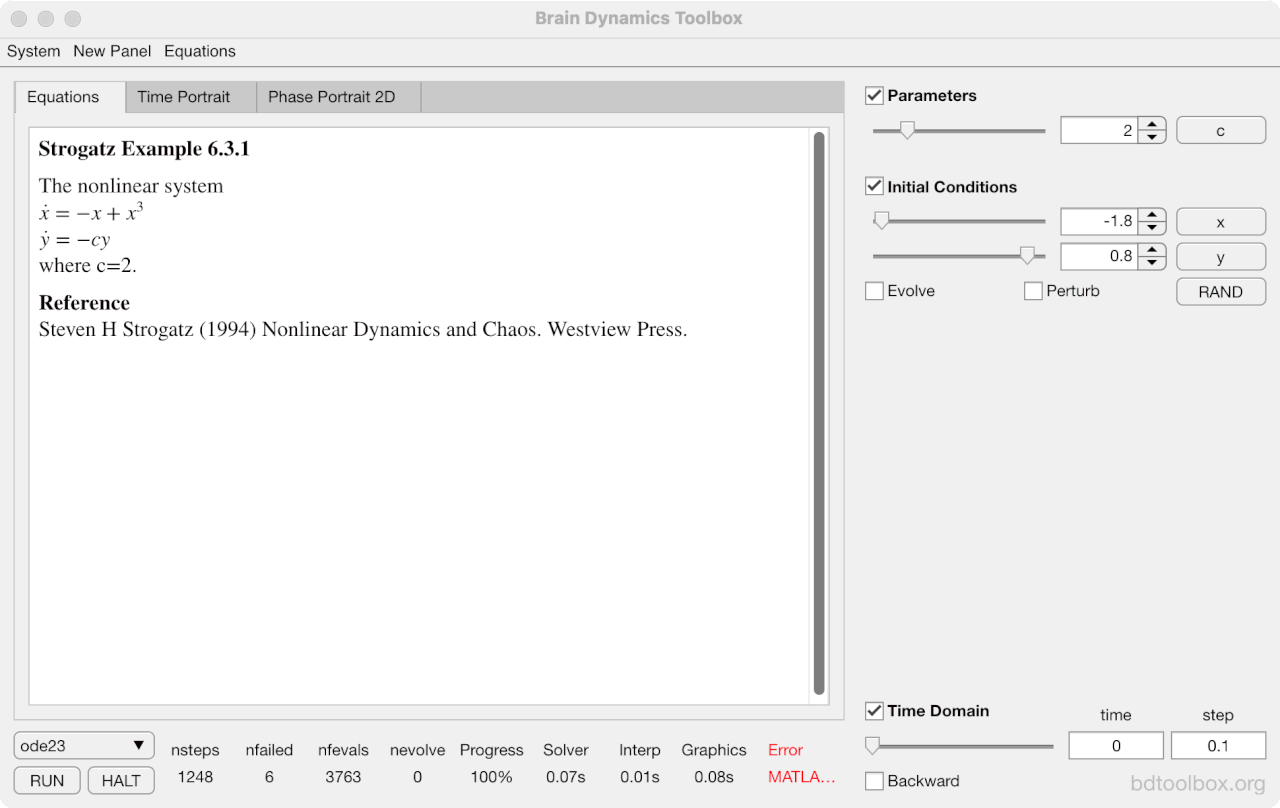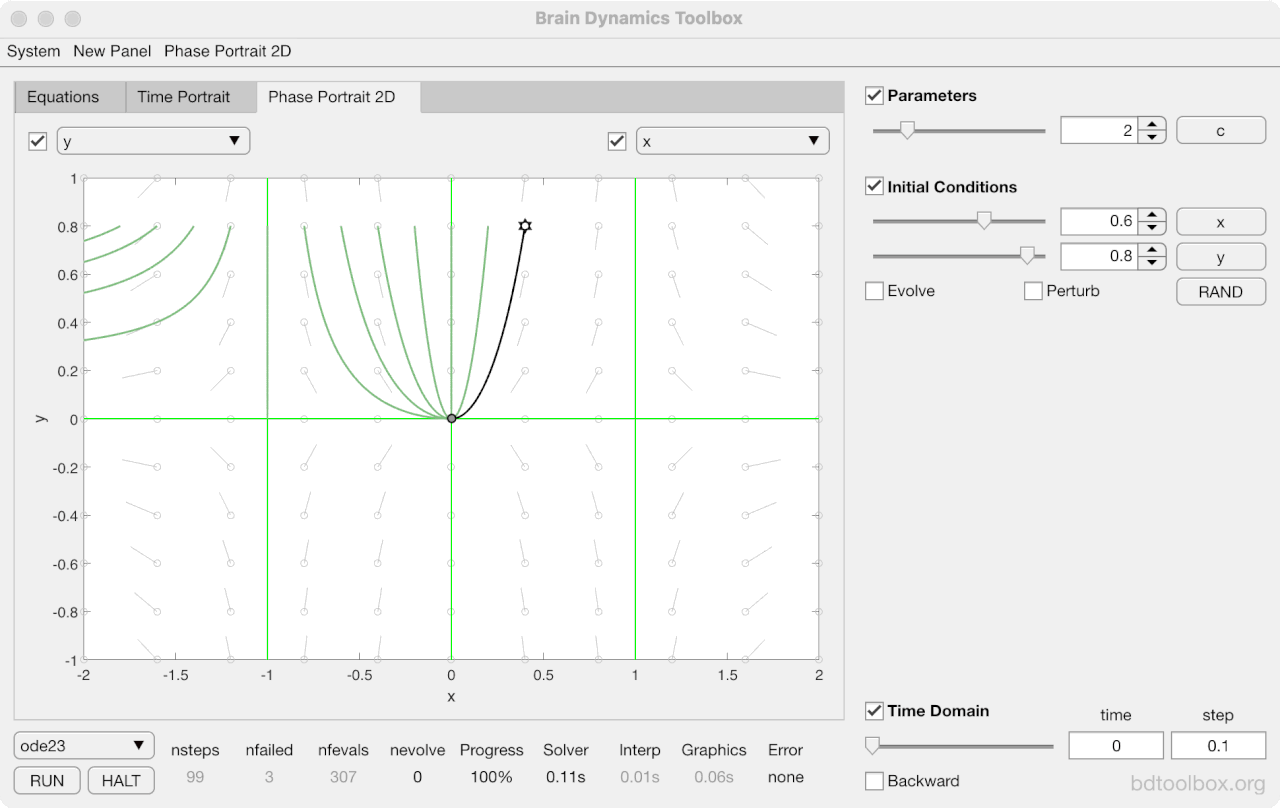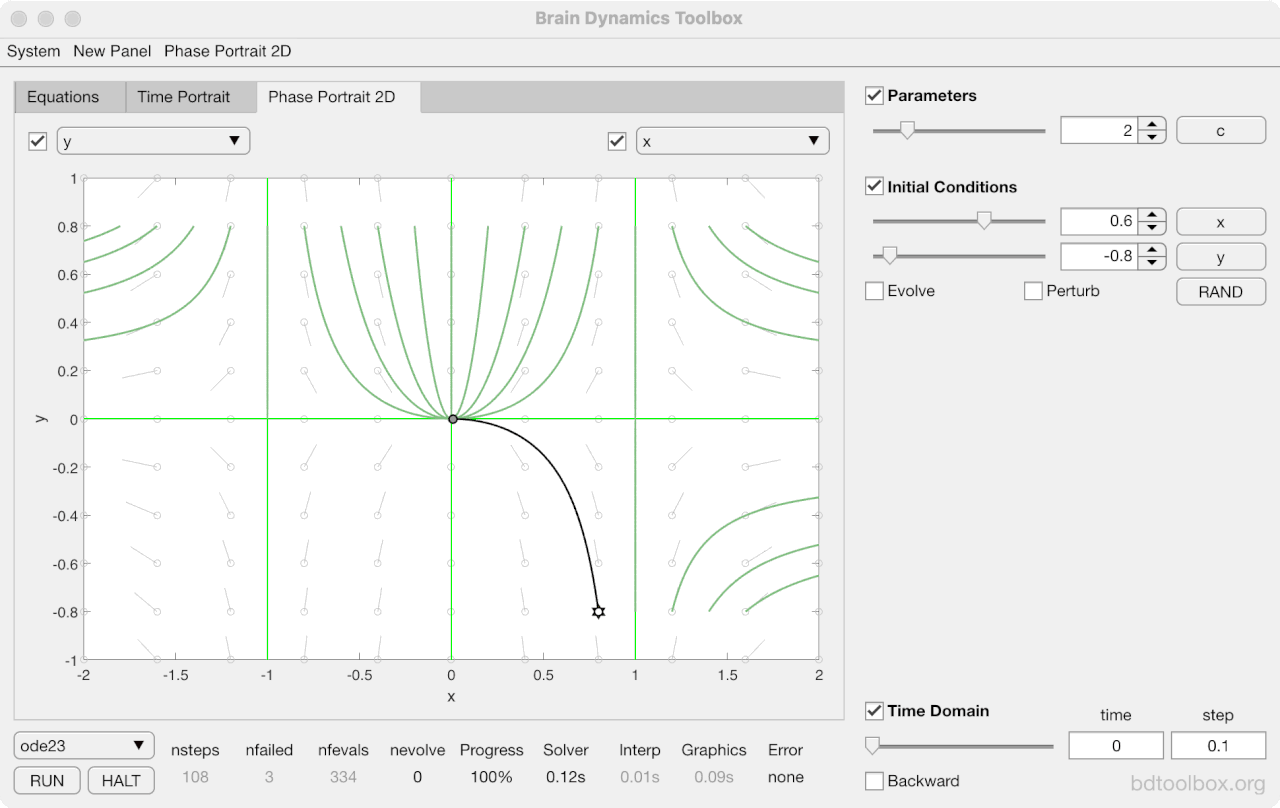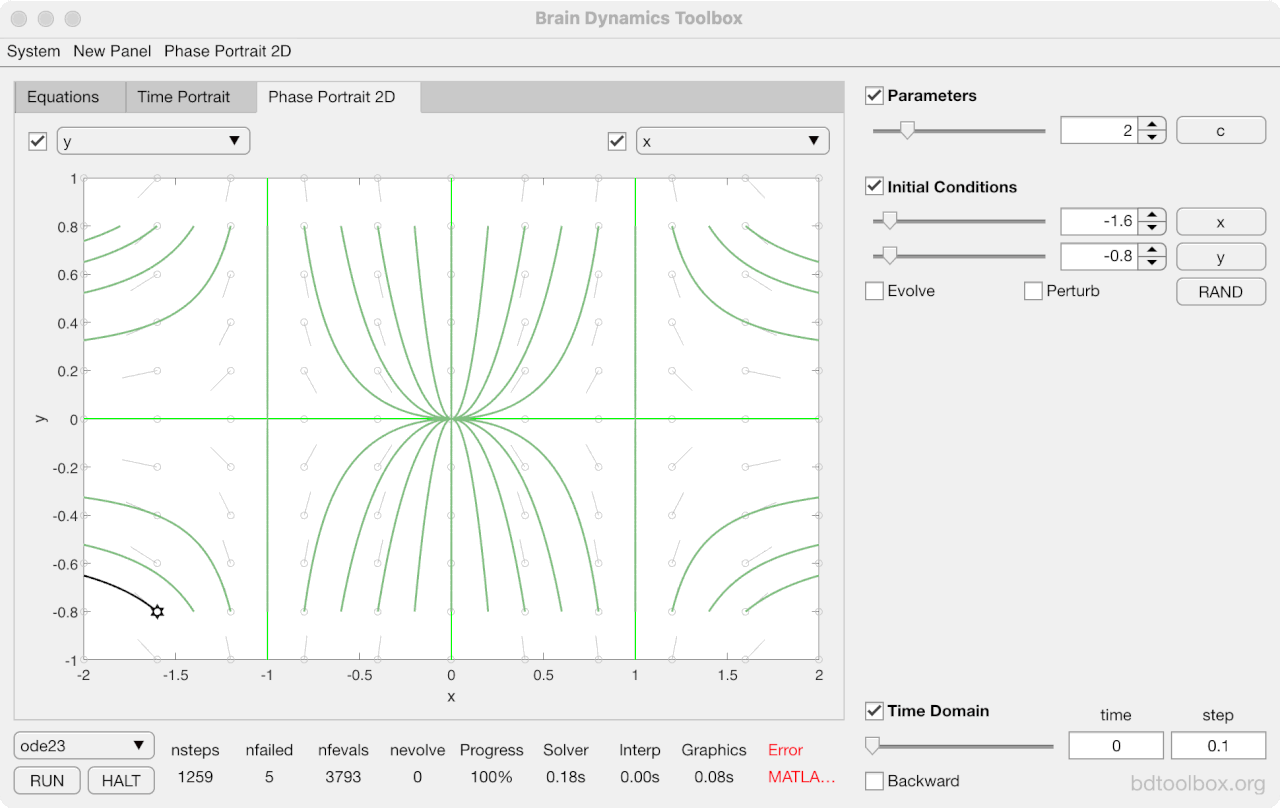
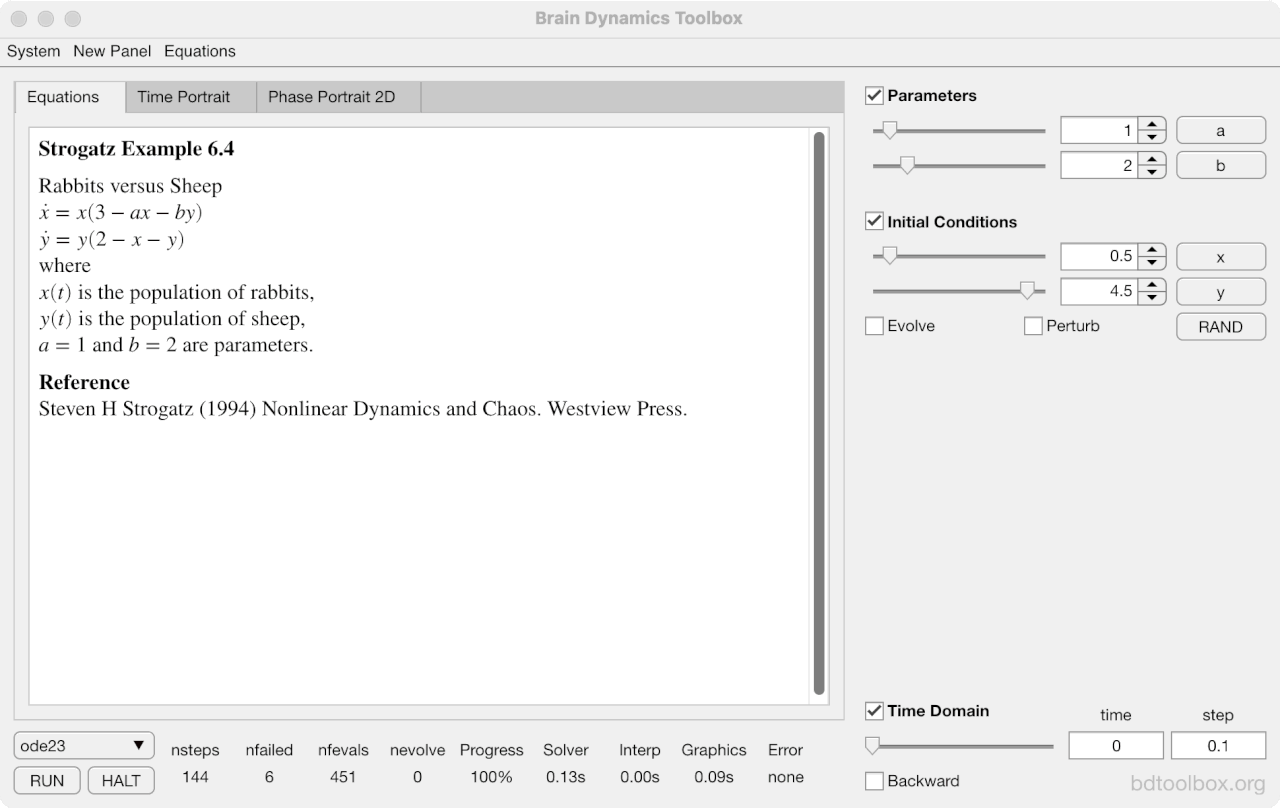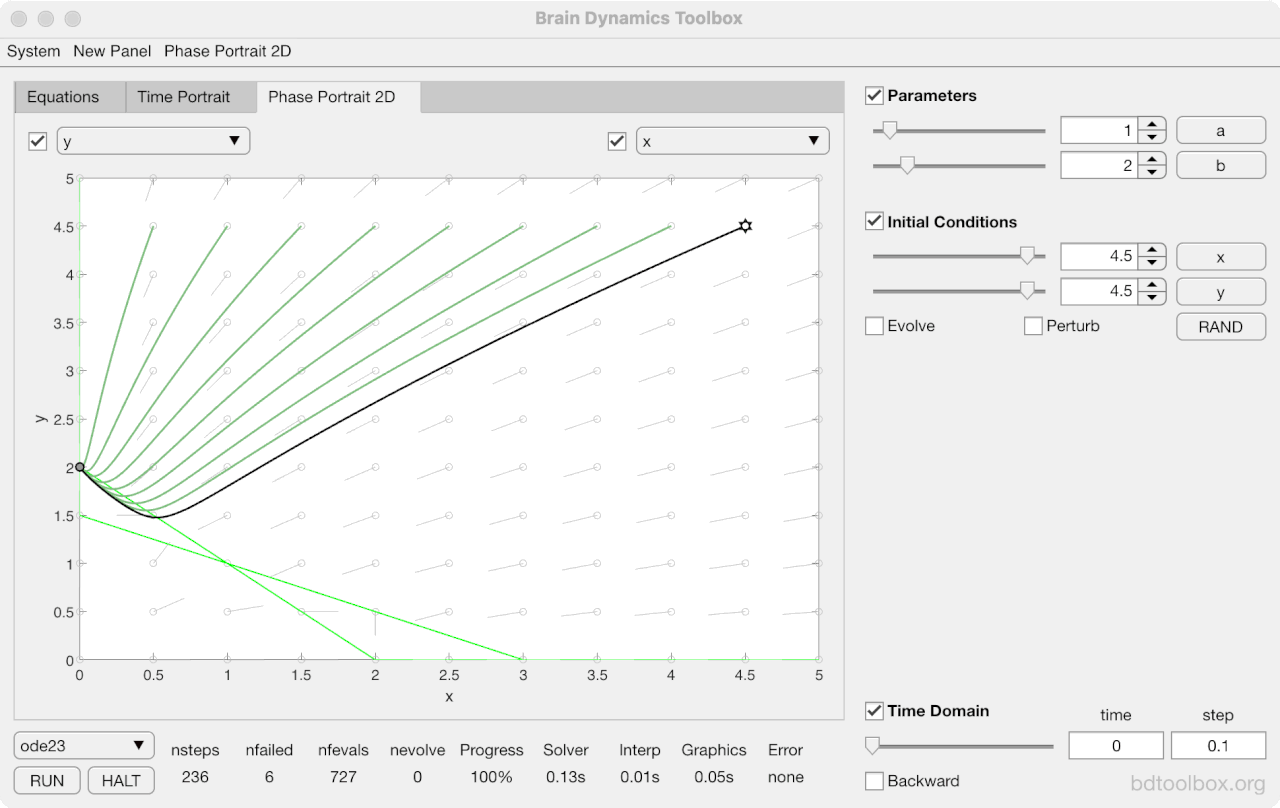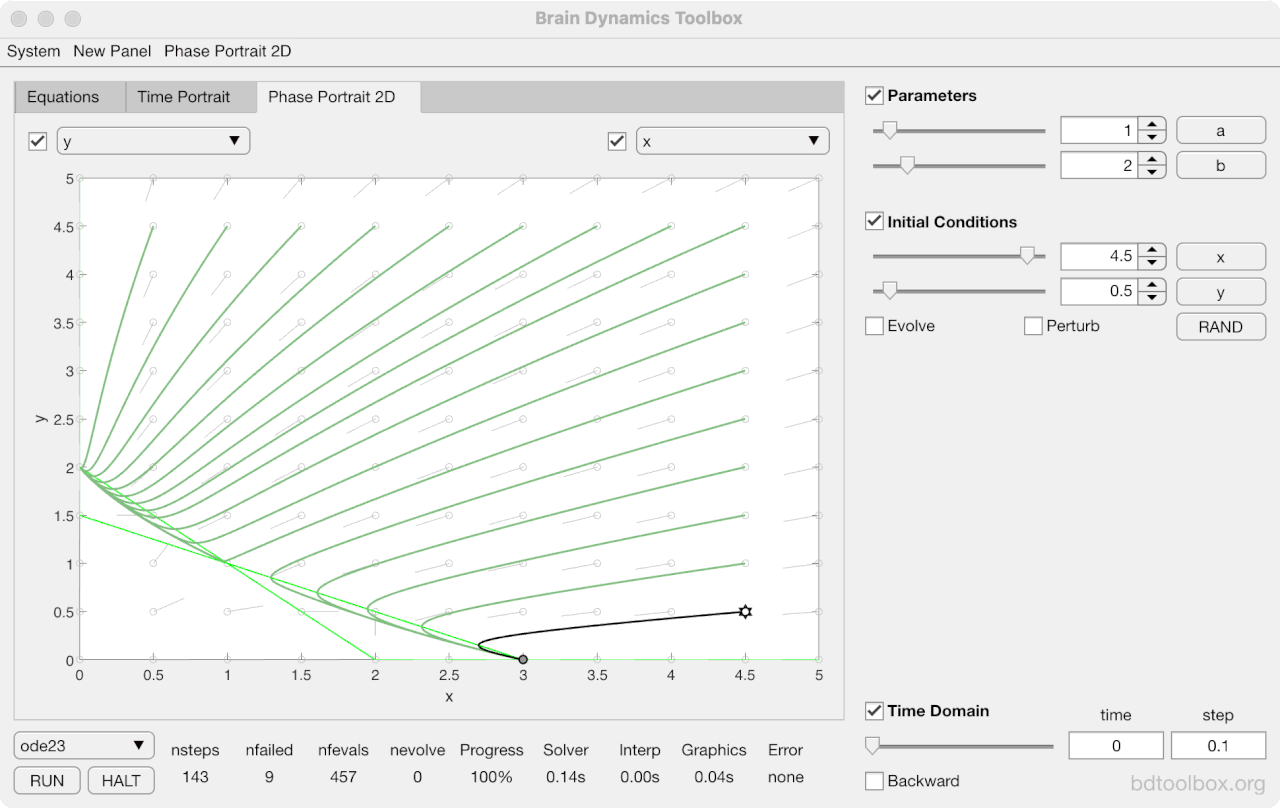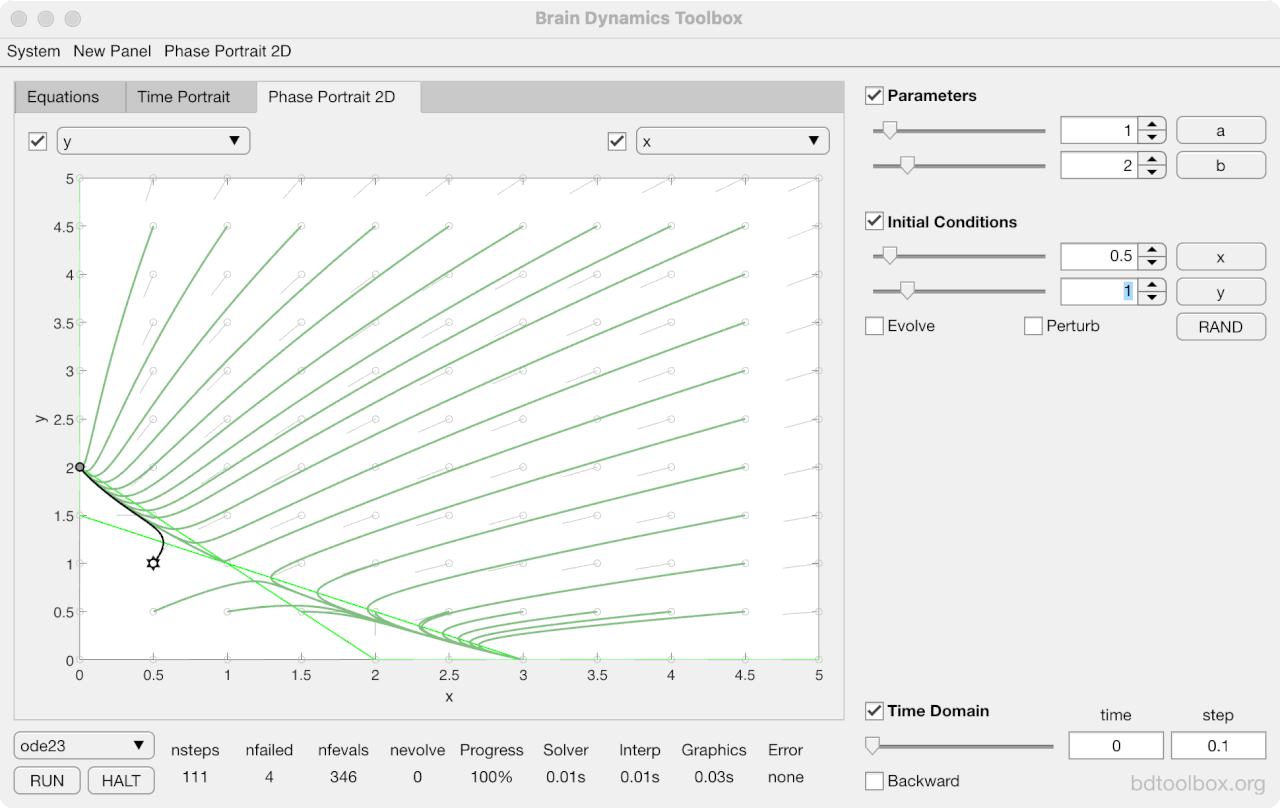
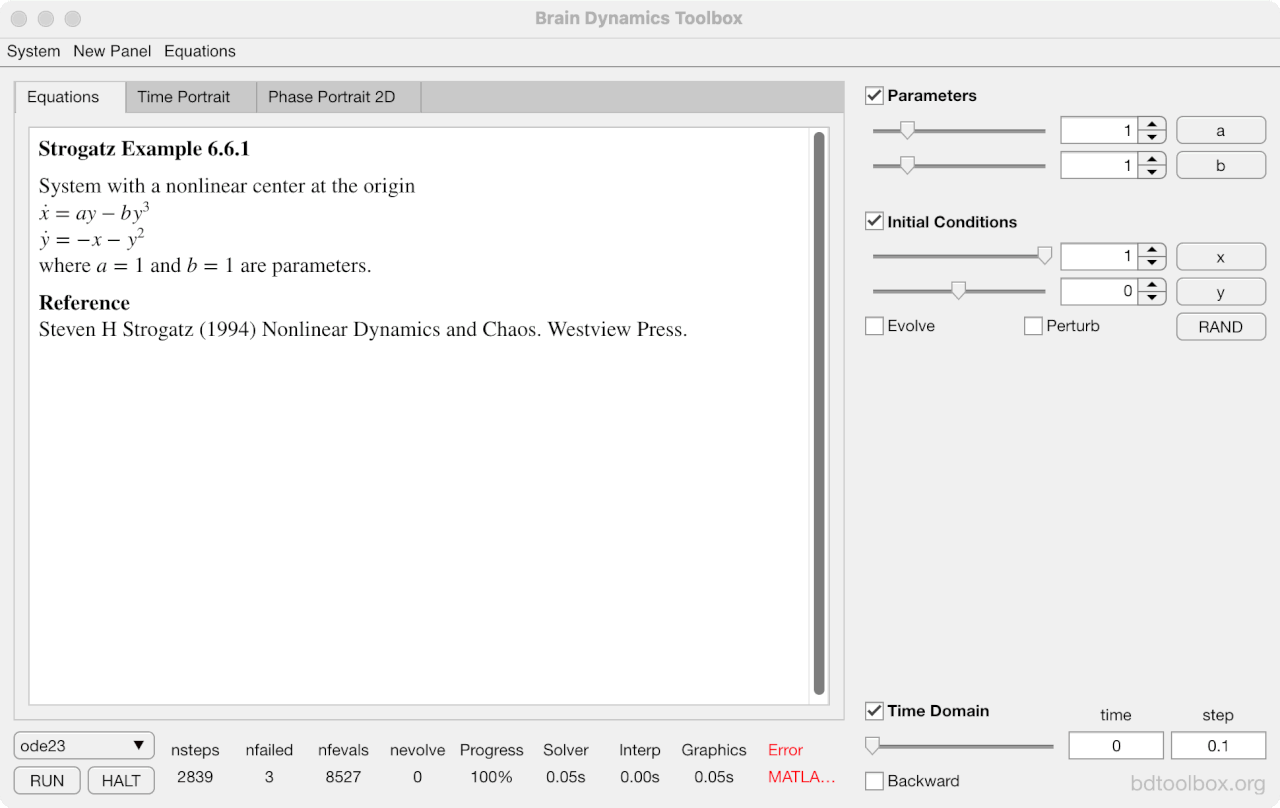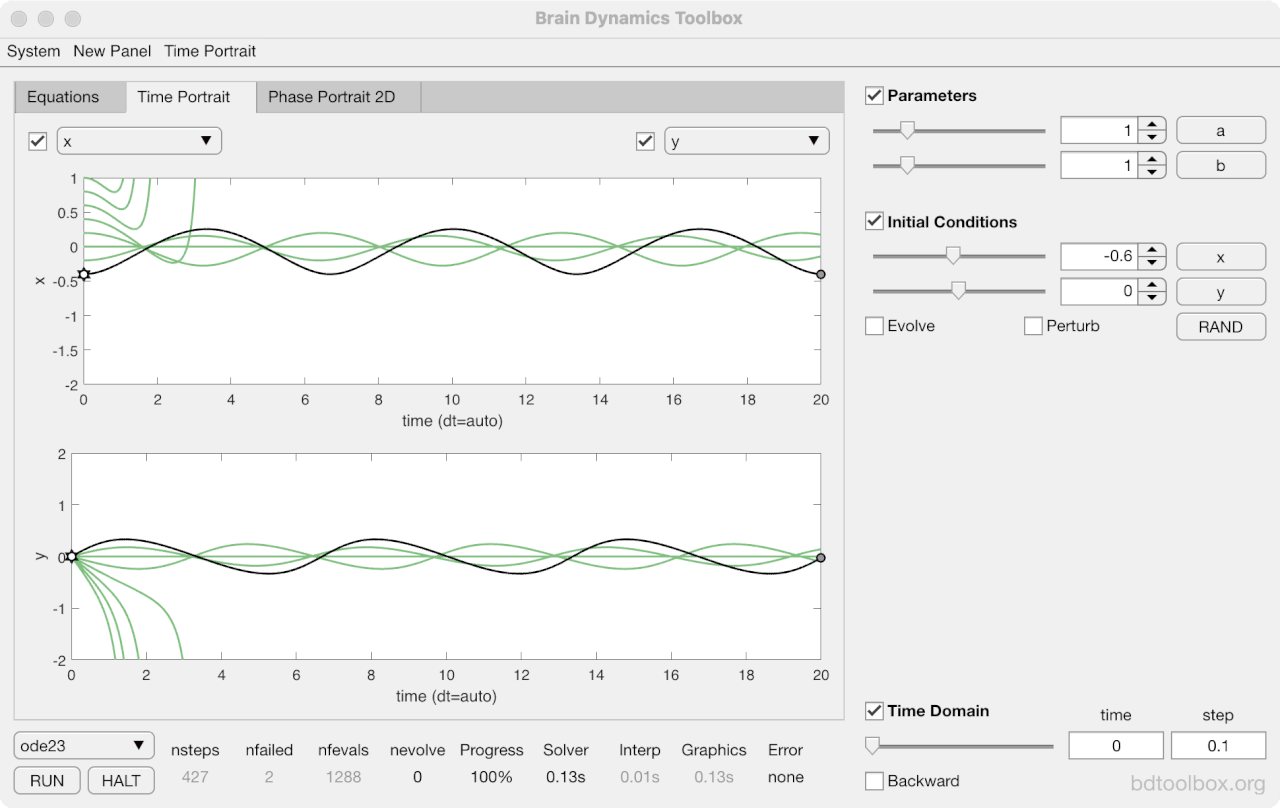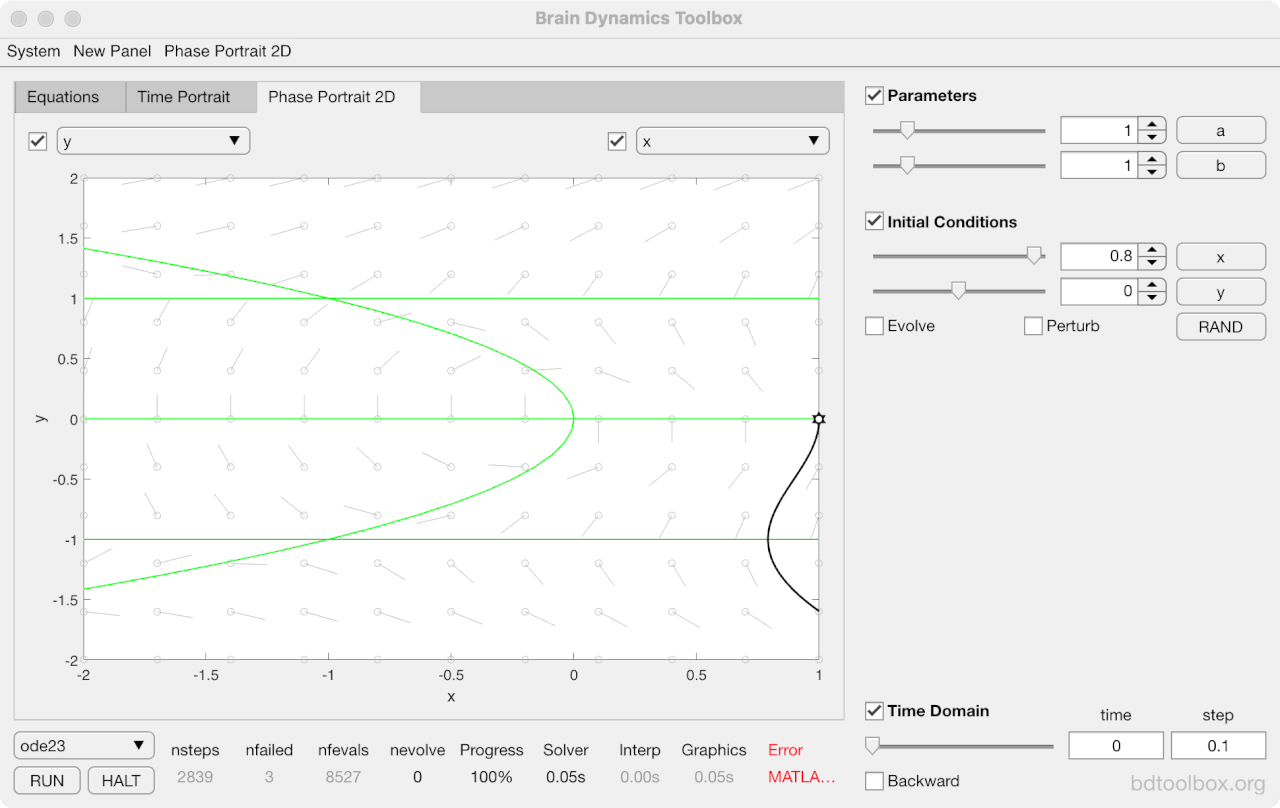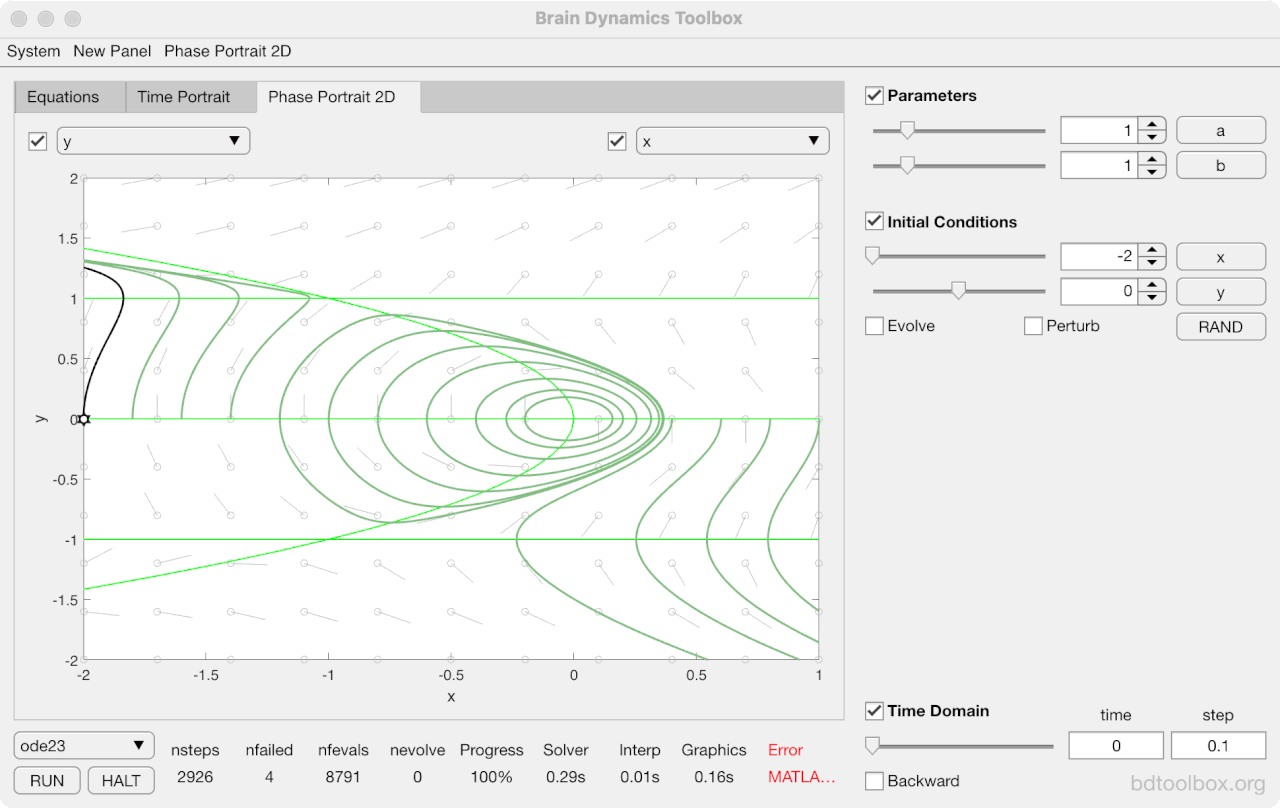
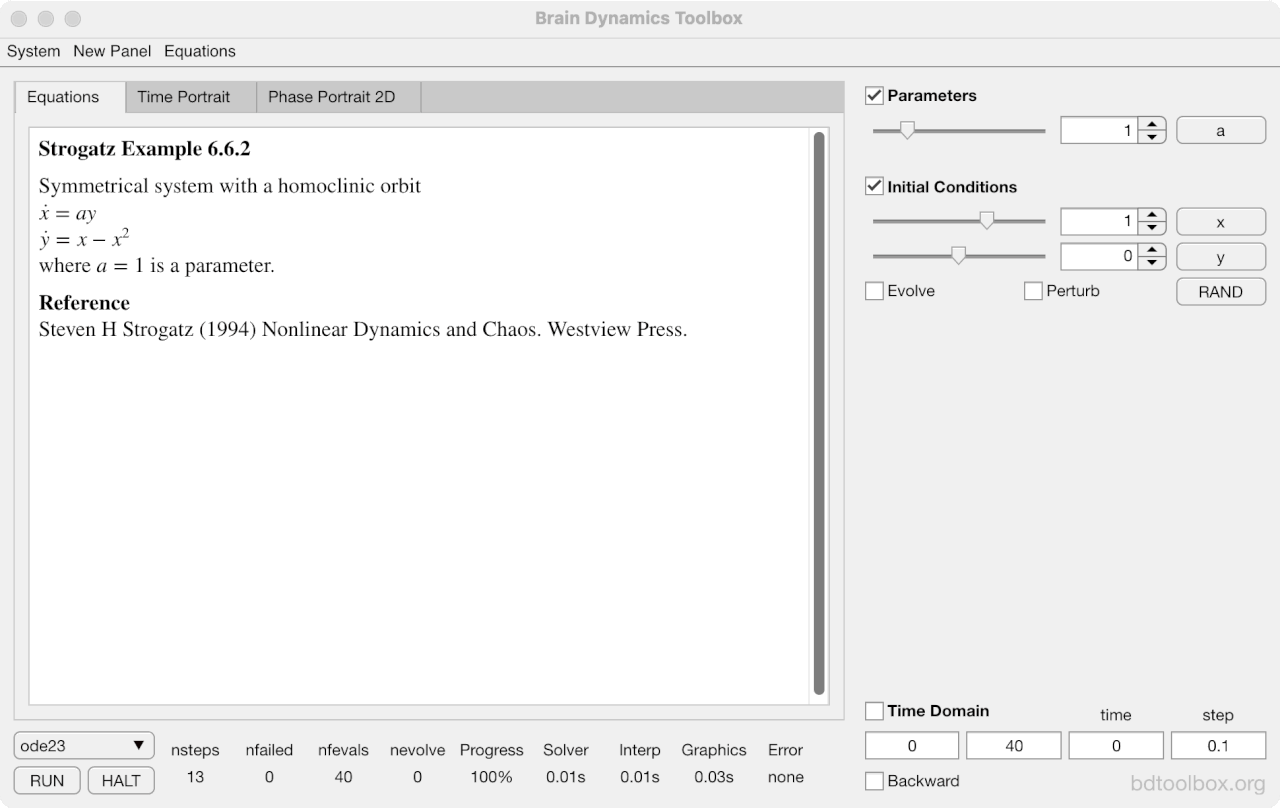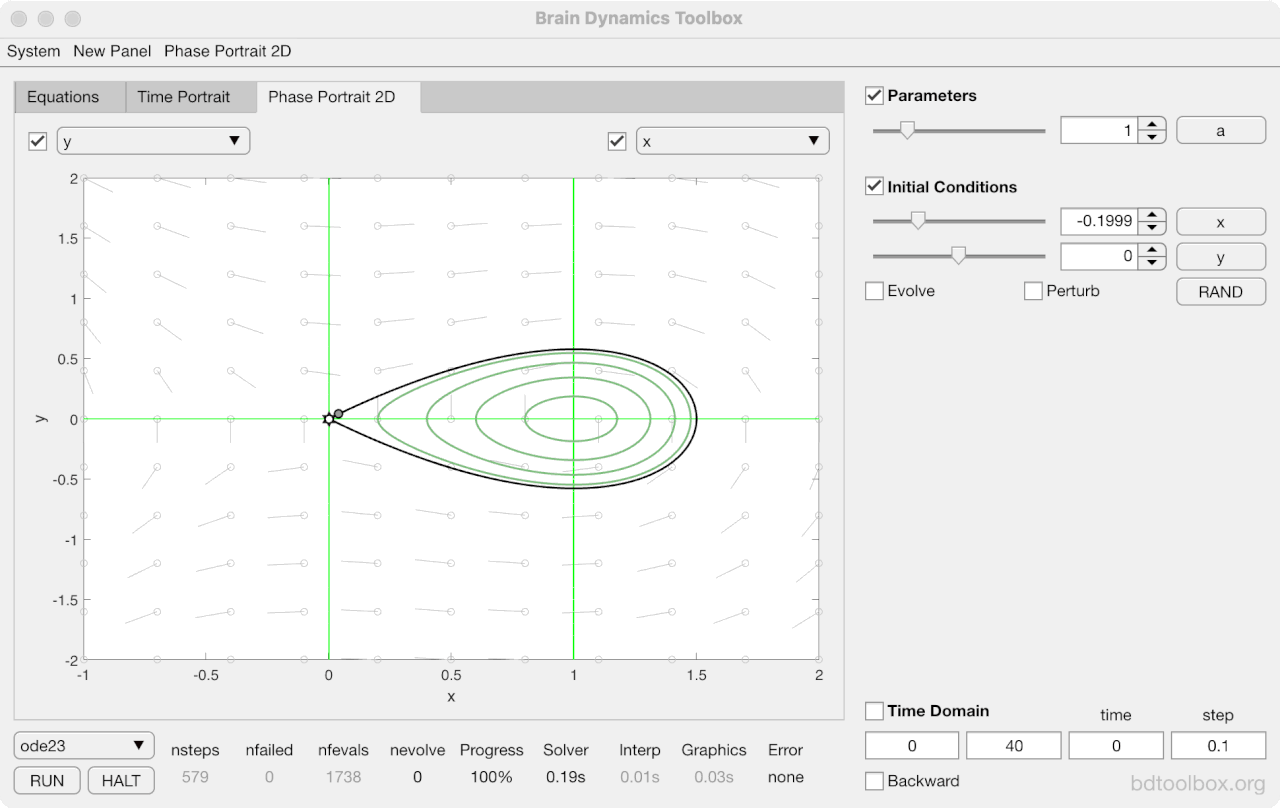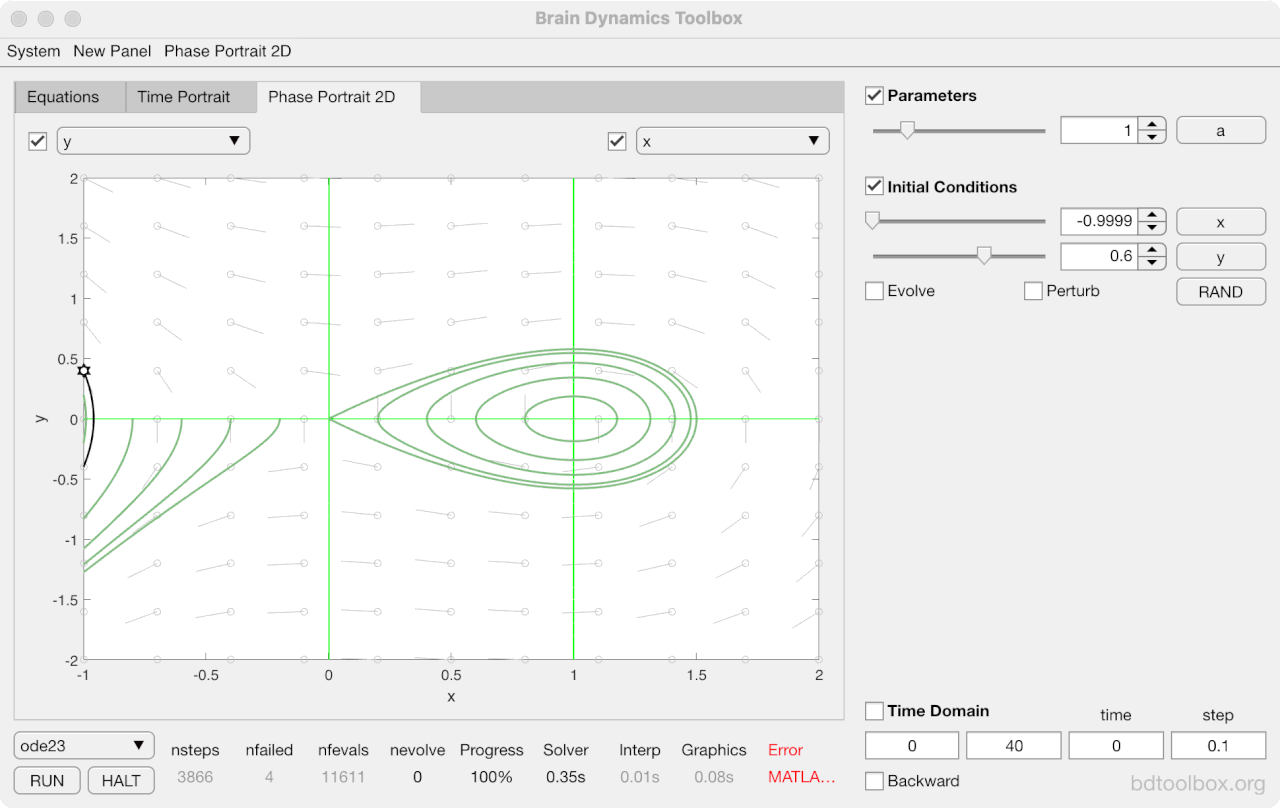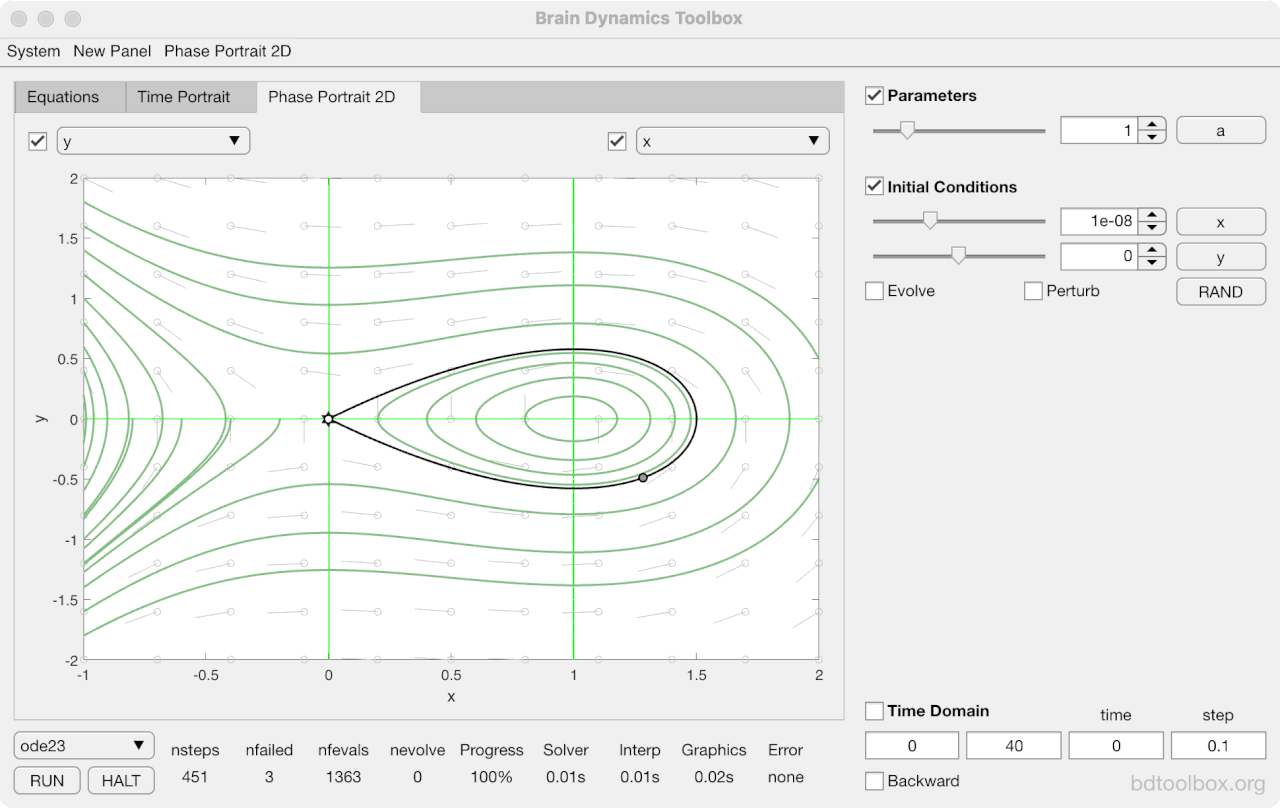
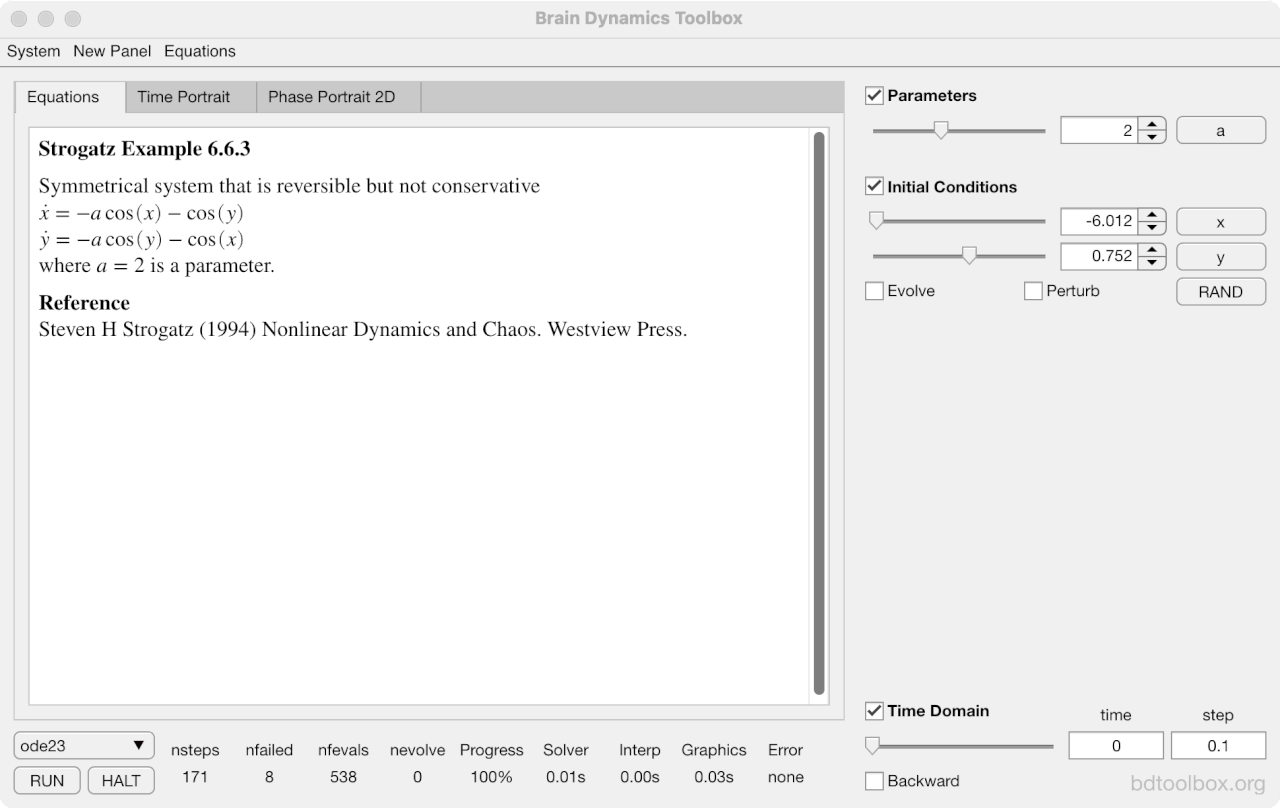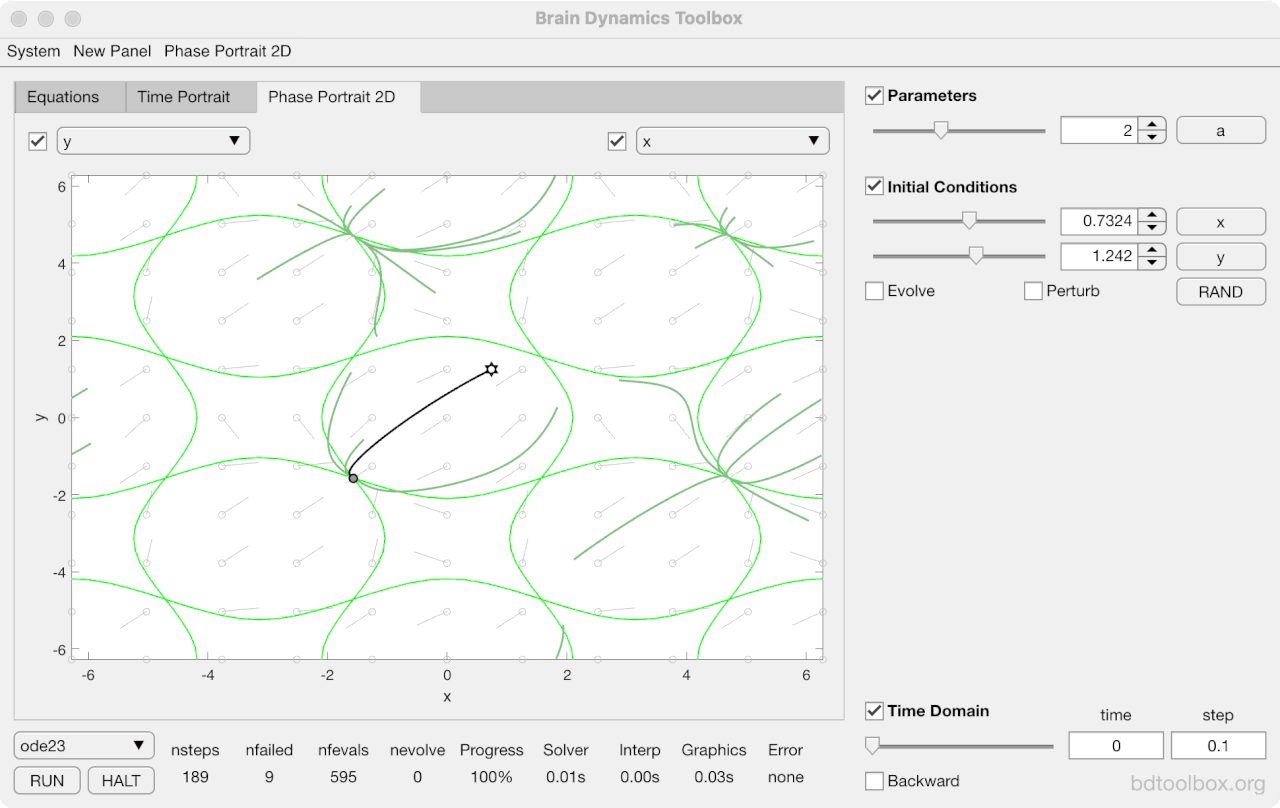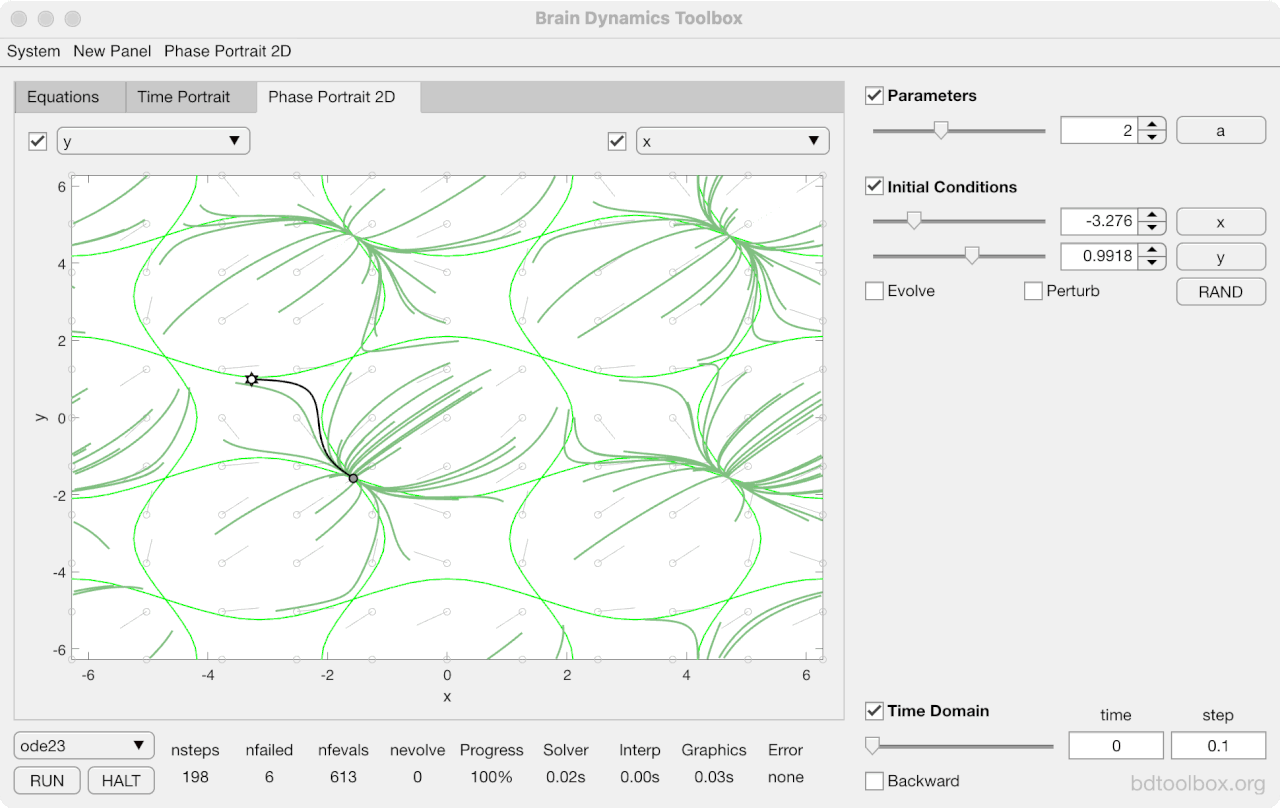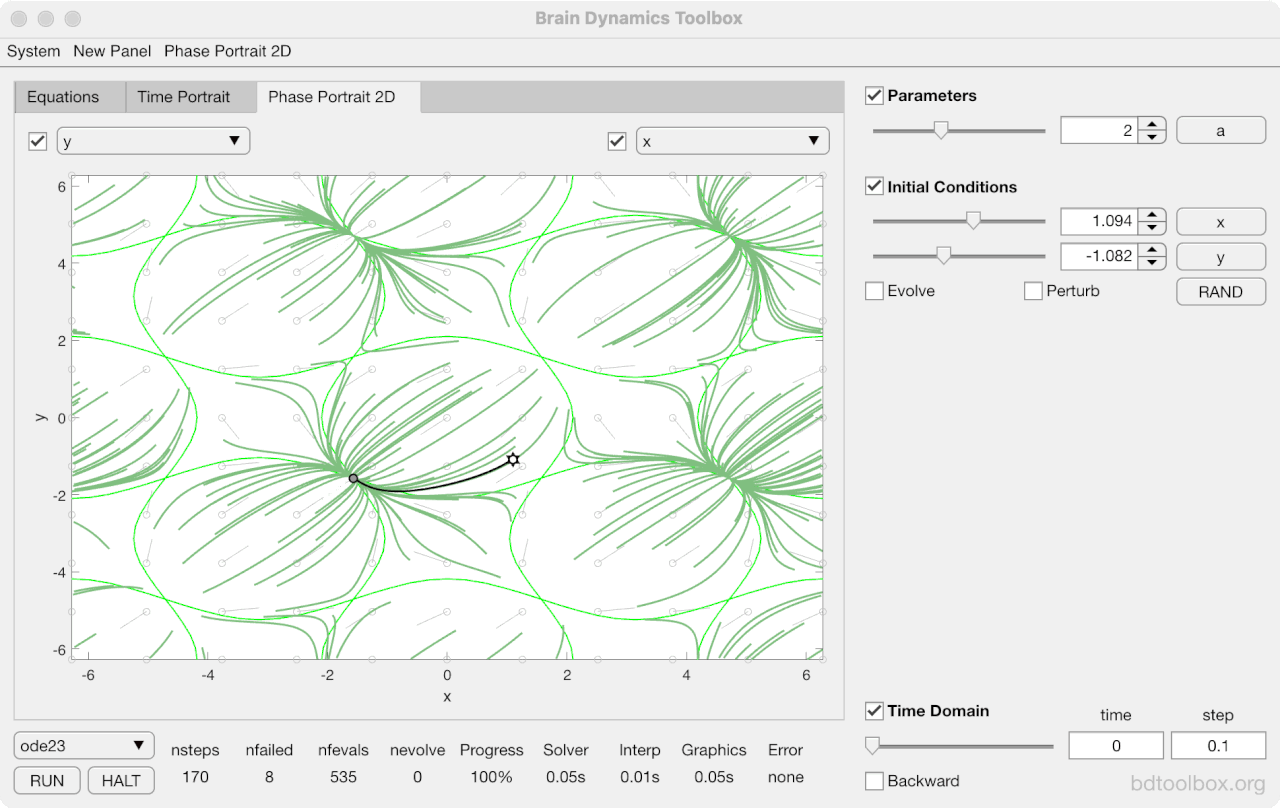
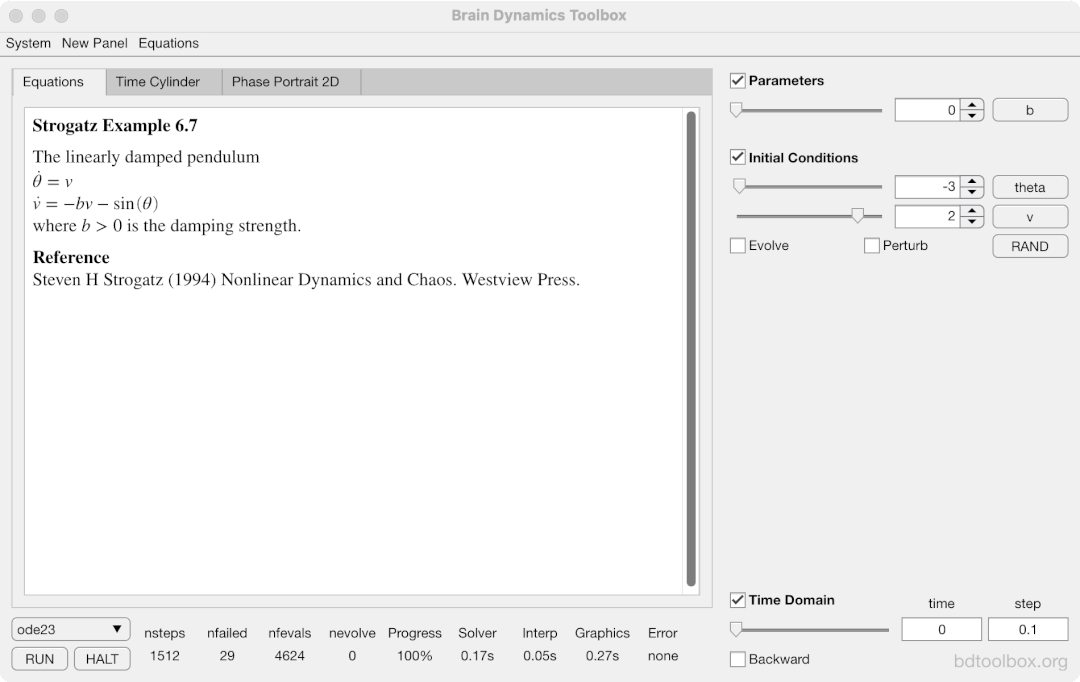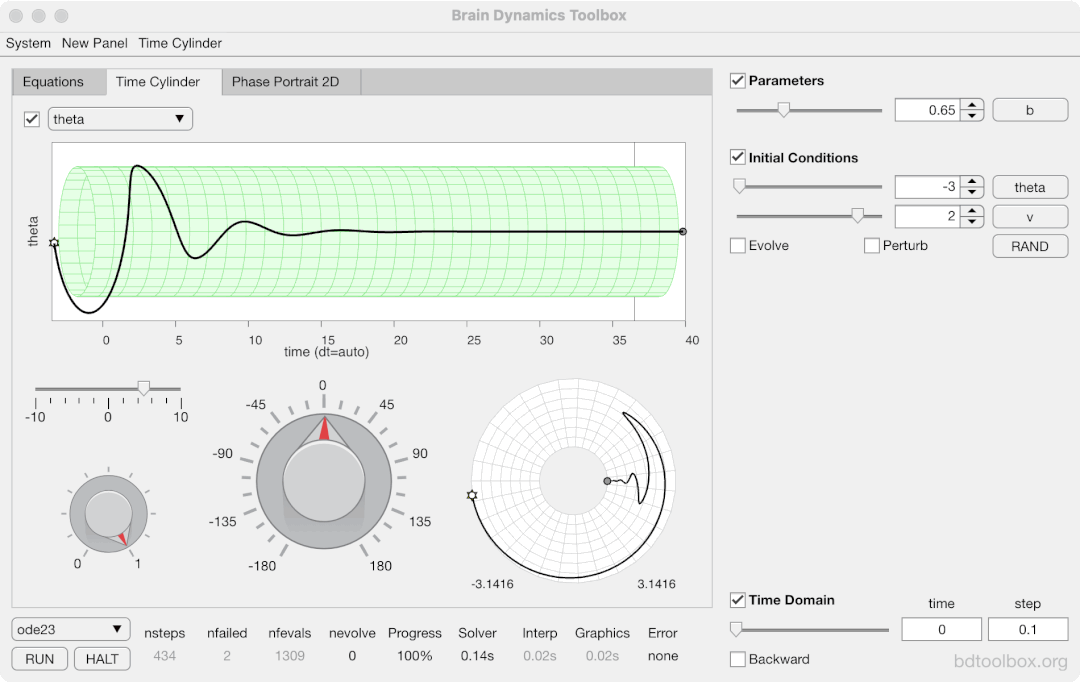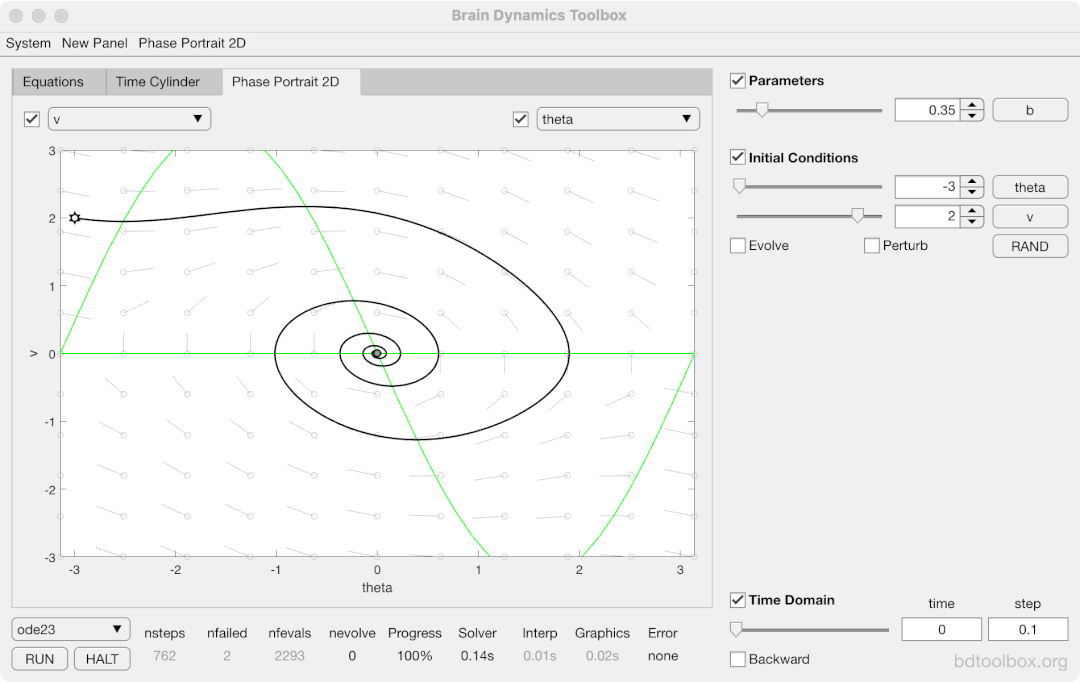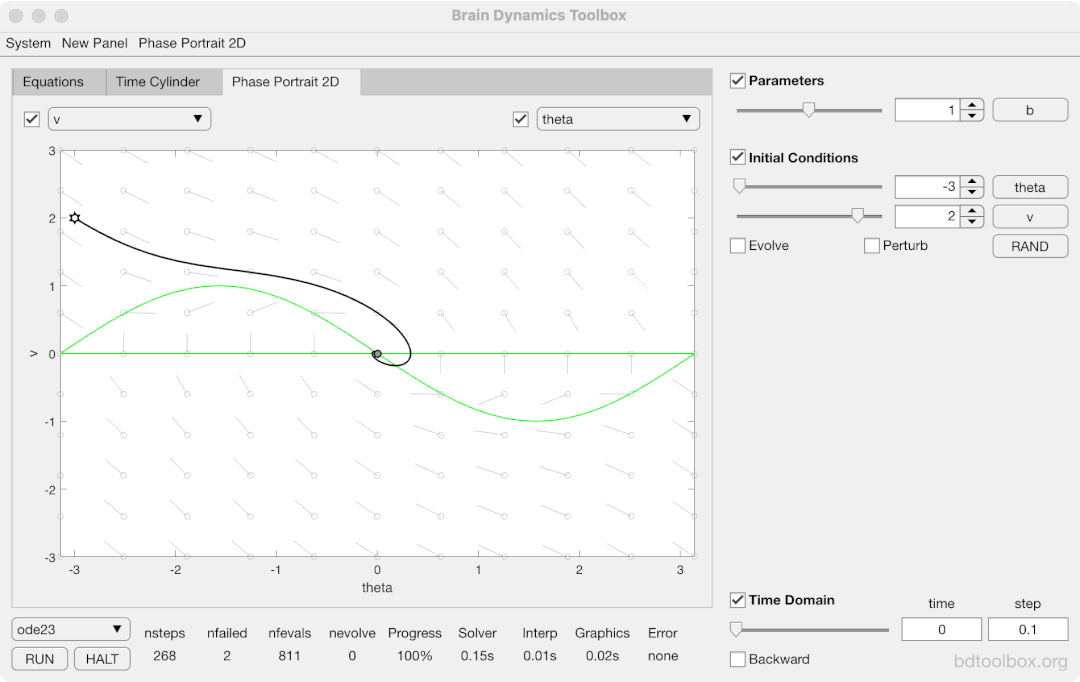
Strogatz Textbook

Selected examples from the 1st Edition of Nonlinear Dynamics and Chaos by Steven H Strogatz (1999).

	Example 5.1.1. Closed orbits in the simple harmonic oscillator.
	Example 5.1.2. A pair of uncoupled linear equations.
	Example 5.2.5. A degenerate node has only one eigenvector.
	Example 5.3.1. Love affairs.
	Example 6.3.1. Saddles and stable nodes.
	Example 6.4. Rabbits versus Sheep.
	Example 6.5.2. Particle moving in a double well potential.
	Example 6.6.1. System with a nonlinear centre at the origin.
	Example 6.6.2. Symmetrical system with a homoclinic orbit.
	Example 6.6.3. A symmetrical system that is reversible but not conservative.
	Example 6.7. The linearly damped pendulum.